Doug Dunham
Artists
Doug Dunham
Professor Emeritus of Computer Science
Dept. of Computer Science, University of Minnesota Duluth
Duluth, Minnesota, USA
Statement
The goal of my art is to create aesthetically pleasing repeating patterns in the hyperbolic plane. These patterns are drawn in the Poincare circle model of hyperbolic geometry, which has two useful properties: (1) it shows the entire hyperbolic plane in a finite area, and (2) it is conformal, i.e. angles have their Euclidean measure, so that copies of a motif retain their same approximate shape as they get smaller toward the bounding circle. Most of the patterns I create exhibit characteristics of Escher's patterns: they tile the plane without gaps or overlaps, they are colored symmetrically, and they adhere to the map-coloring principle that no adjacent copies of the motif are the same color. These patterns are designed using an interactive drawing program and then rendered by a color printer. The two major challenges in creating these patterns are (1) to design appealing motifs and (2) to write programs that facilitate such design and replicate the complete pattern.
Artworks
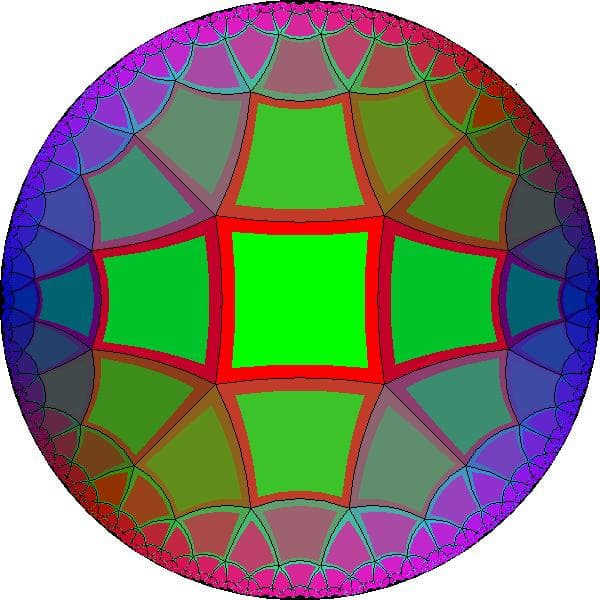
Smoothly Colored Squares 45
11 by 11 inches
Color printer
2010

Randomly Colored Squares 46
11 by 11 inches
Color printer
2010

Randomly Colored Circles 46
11 by 11 inches
Color printer
2010