2012 Joint Mathematics Meetings
Jo Niemeyer
Artists
Statement
The basis of my work as an artist is the connection between art and nature, between the artistic action and the experimental work. This means that my artistic production which is fundamentally based on natural principals and measures is nothing more than a sequence of experimental steps which implies given and objective criteria and subjective factors in the same way. My main interest is directed to the perception of space, time, distances and proportion and forms the synthesis between art and nature which implies in the end a dialogue between man and nature...
Artworks
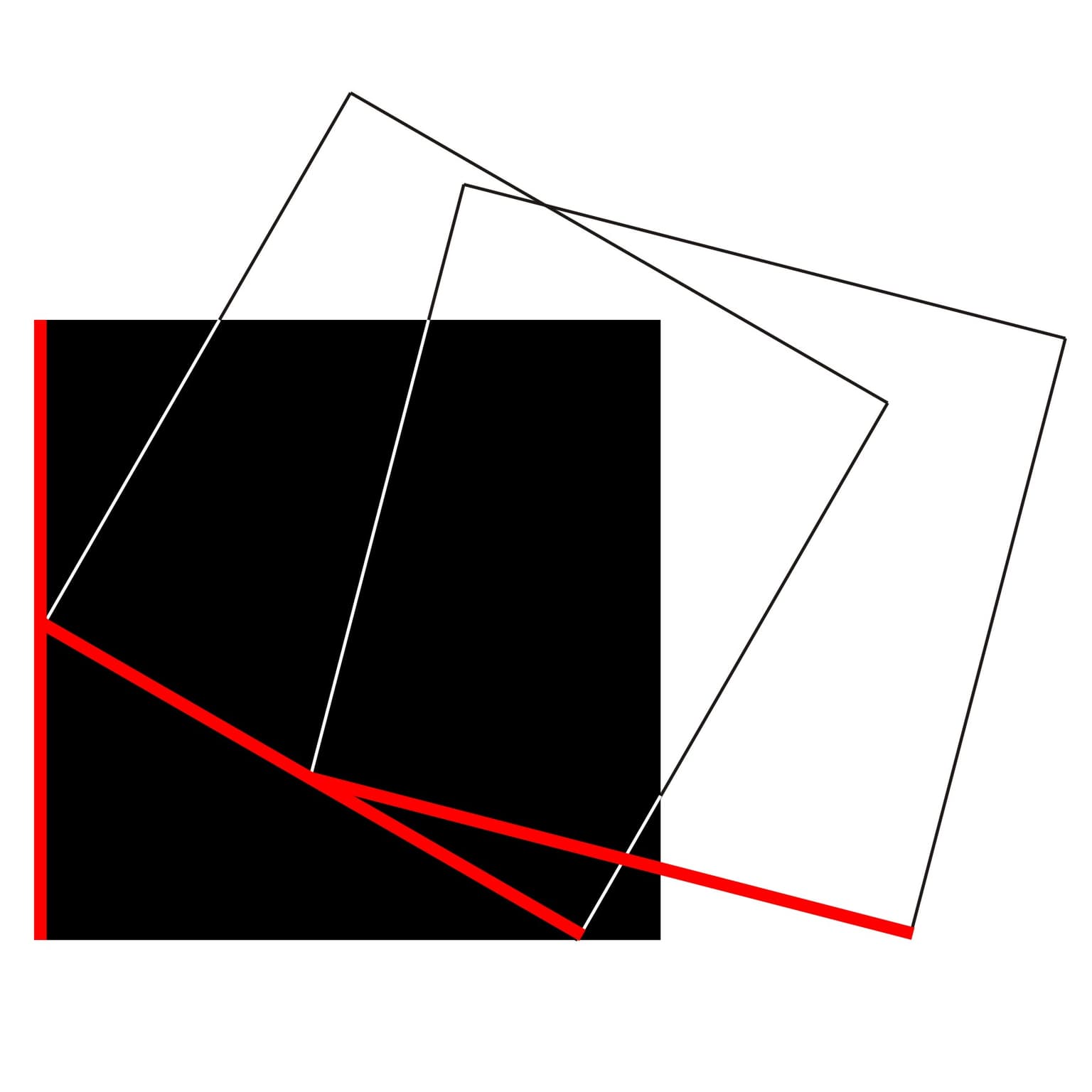
CONSTRUCTION
20" x 20"
Archival Inkjet Print
2011
The number phi (1,618..) is, alongside pi, one of the most amazing numbers of all. It is known as the “Golden Section” and has, time and again, fascinated scientists and mathematicians in particular, as well as architects and artists. This number plays a role not only in the symmetrical structure of blossoms in the plant world, but also in the structure of spiral galaxies and in the symmetry of quasicrystals, as well as in the art of Leonardo da Vinci and in music, for example in some pieces by Béla Bartók. The geometry of the Cheops pyramid exhibits the Golden Section with particularly impressive exactness, although we do not know with certainty whether or not the ancient Egyptians were aware of this ratio.
The classic construction of the Golden Section due to Euclid, which is the usual one to the present day, is somewhat cumbersome. Jo Niemeyer set out to find an alternative construction and in 2011 he discovered a way to achieve the Golden Section with only three equally long line segments with a mark at their centre, using what he calls “simplified rules”.
His construction is so clear in its logical simplicity that its mathematical proof based on the two resulting half-sized triangles is almost immediate. Here we thus have an example of mathematics resulting from concrete art instead of the other way round!