Robert Fathauer
Artists
Robert Fathauer
Owner
Tessellations
Apache Junction, Arizona, USA
Statement
I’m fascinated by beautiful and complex forms both in mathematics and in the natural world. Combining mathematics with artistic creativity allows me to explore and express these ideas in unique images and forms.
Artworks
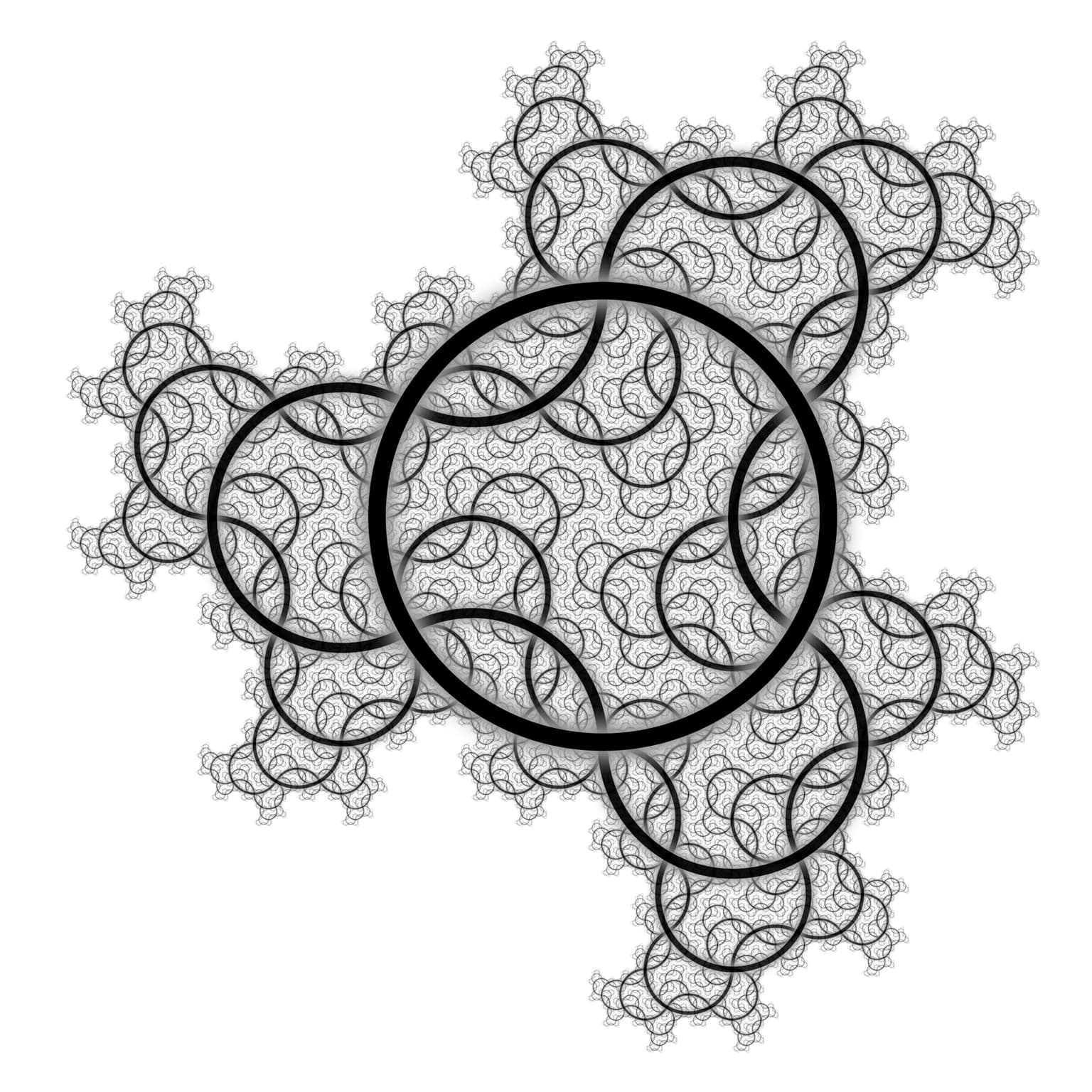
Iterated Curve
18" x 18"
Archival inkjet print
2012
This print shows the first ten generations of a fractal curve generated by an iterative process. The curve uniformly fills the space within its boundaries in a manner similar to a Hilbert curve, while the boundary itself is also a fractal curve. This is a circular version of a curve that is found in Benoit Mandelbrot's classic book "The Fractal Geometry of Nature".

Rhombic Dodecahedron
4" x 4" x 4"
Ceramics
2013
The grooves on this rhombic dodecahedron separate the surface into eight triangular pyramids, illustrating the relationship of the rhombic dodecahedron to the octahedron. The equilateral-triangle bases of the triangular pyramids would form a regular octahedron. The alternate grooved and smooth regions further illustrate the fact that an octahedron can be two colored.
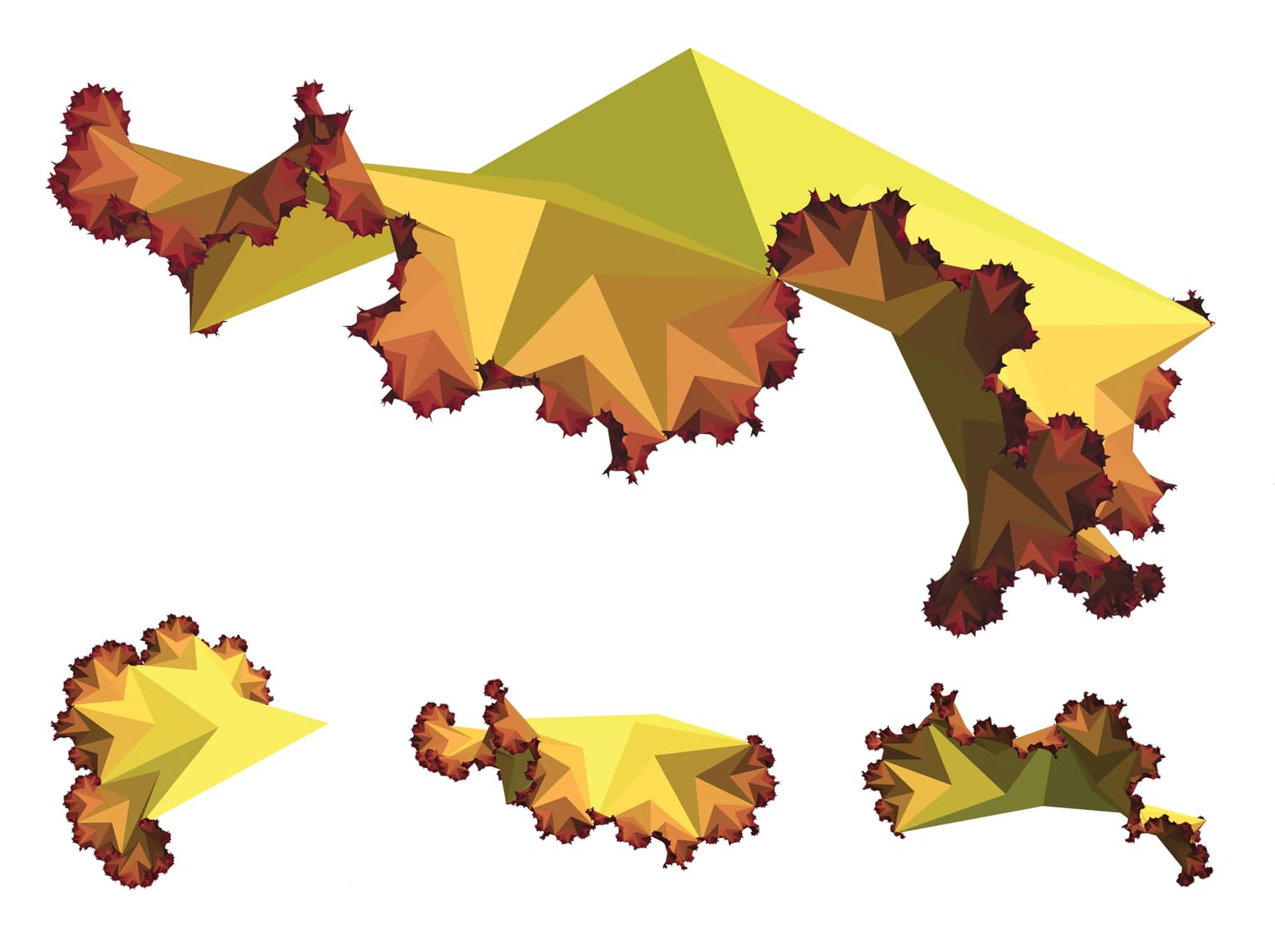
Hyperbolic Fractal Tiling No. 1
18" x 24"
Archival inkjet print
2012
This digital artwork features four views of the same three-dimensional object, a fractal tiling in which every tile is a similar dart shape. The starting point is a pair of tiles matched along one long edge. A pair of smaller tiles is fit into each of the V-shaped openings in these starting tiles. The sum of the angles at each vertex where two of the smaller tiles meet a larger tile is greater than 360 degrees, so the three tiles cannot lie in the same plane. The pairs of smaller tiles alternately buckle up and down to accommodate the fit. This same simple rule is applied repeatedly through ten generations, resulting in the object shown. This object was created in Mathematica, and PhotoShop was used to create the montage. This is a demonstration of the way in which a complex organic structure can result from a simple set of rules being applied over and over again to a simple starting structure. The resulting object is an intriguing blend of the organic and the geometric.