Hartmut F. W. Höft
Artists
Hartmut F. W. Höft
Professor of Computer Science, emeritus
Eastern Michigan University
Ann Arbor, Michigan, USA
Statement
I like to experiment with simple planar geometric figures. Starting with one outline I move it, rotate it, and change its proportions. This process generates a sequence of intersecting outlines. With my images I want to demonstrate that applying elementary planar transformations to one simple shape produces complexity that can mask how the images were generated. One special planar form is the ellipse: it is convex, has mirror symmetries and a shape that is easily manipulated through its two semi-axes. Furthermore, our eyes immediately recognize its outline. The centers of the ellipses are moved along a closed, planar curve that I think of as the spine of the figures. A general (polar) form of the equations that I use for the spines is r(t) = s + sin^n(n t) + cos(k t), where s, n, and k usually are integer valued parameters. Since the spine is not drawn, this one fundamental aspect of the images remains hidden to be discovered by a viewer. All images are mathematically planar.
Artworks
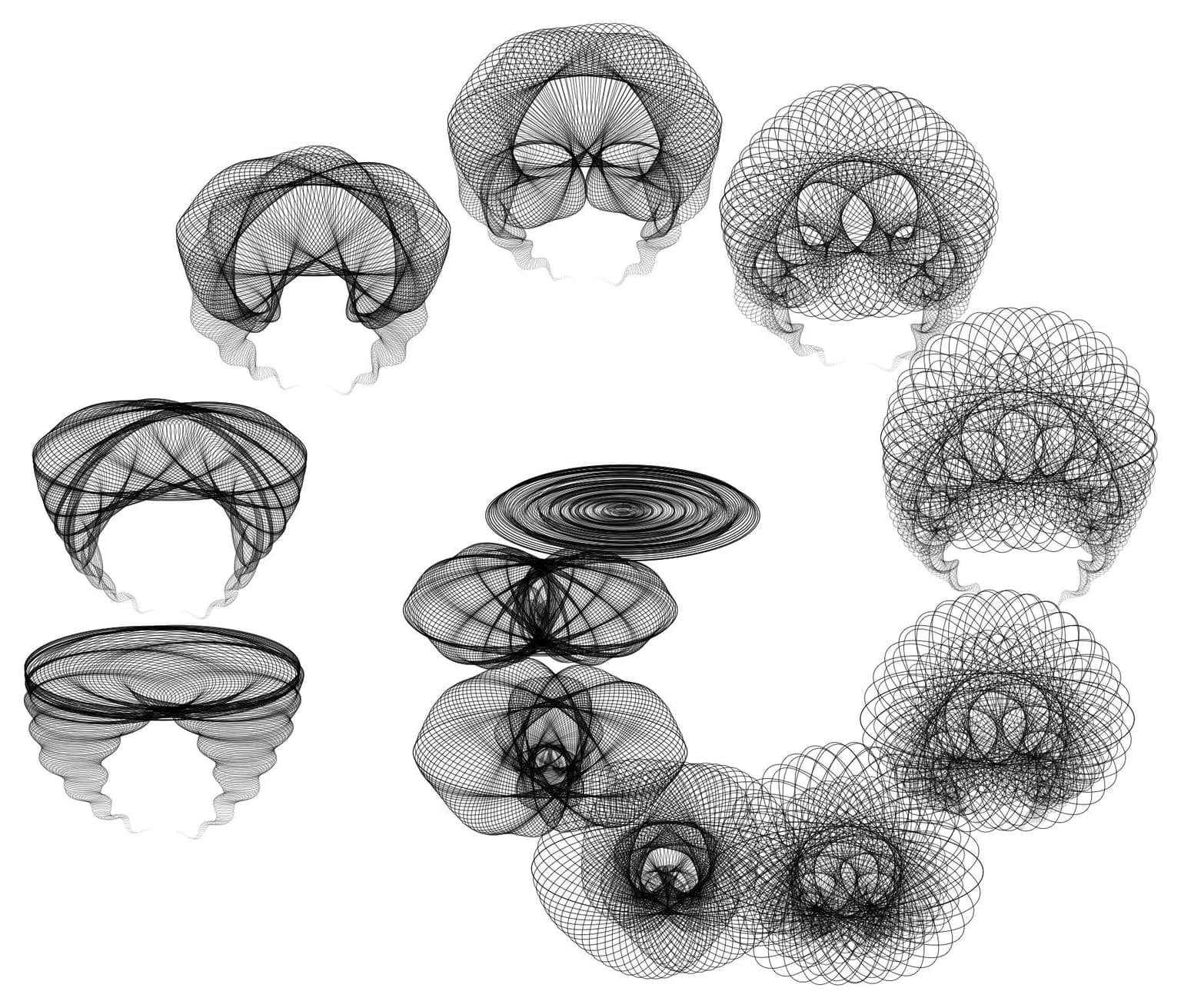
Evolution of Twin Tornados
7.5 x 9 (10.5 x 12 framed) inches
archival photographic digital paper
2013
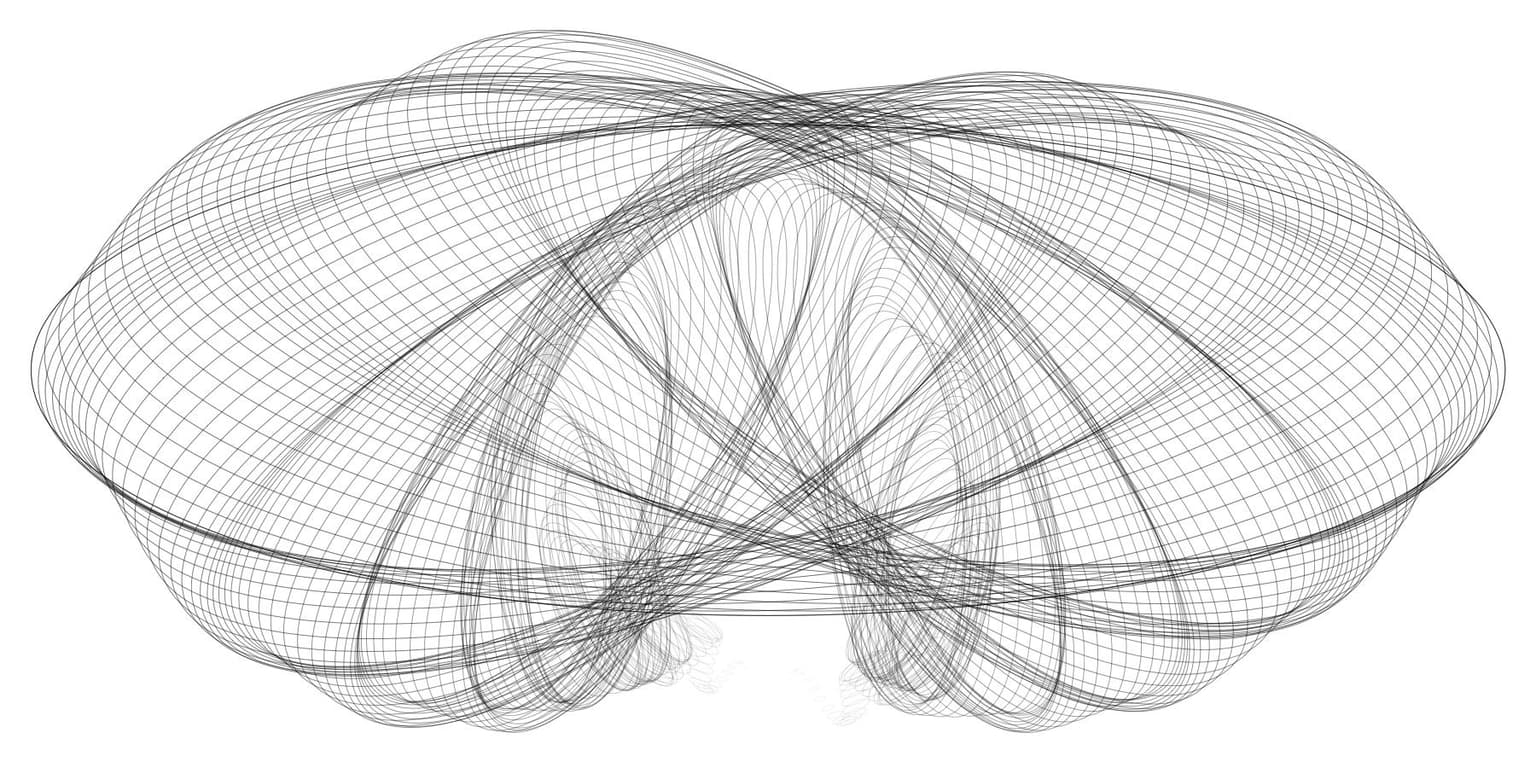
Billowing Net (Study 17)
5 x 10 (8 x 14 framed) inches
archival photographic digital paper
2013

Elliptical Staircase (Study 11)
10 x 7.5 (13 x 10) inches
archival photographic digital paper
2013