Robert Fathauer
Artists
Robert Fathauer
Owner
Tessellations
Apache Junction, Arizona, USA
Statement
I'm endlessly fascinated by certain aspects of our world, including symmetry, chaos, and infinity. Mathematics allows me to explore these topics in distinctive artworks that I feel are an intriguing blend of complexity and beauty. The laws that govern our physical universe can be succinctly expressed by mathematical equations. As a result, mathematics can be seen throughout the natural world, and much of my work plays on mathematical forms in nature.
Artworks
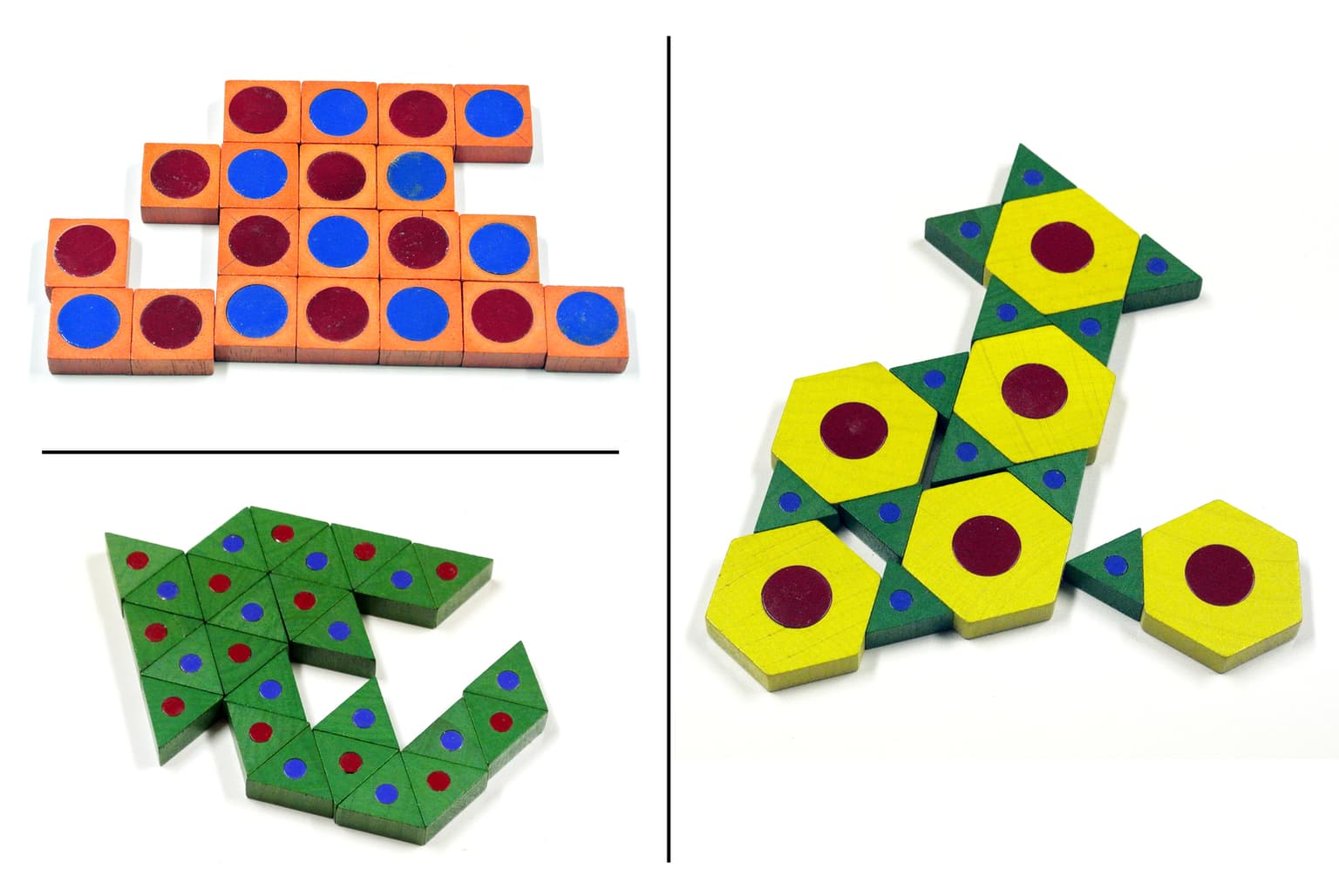
Self-organizing Tiling Art
17" x 20" x 1"
Painted wooden tiles with magnets
2014
This interactive artwork consists of a set of wooden tiles with magnets set in them, along with a framed surface. The user arranges the tiles in a starting configuration and then shakes the frame, allowing the tiles to move around and self organize into tiling clusters. The tiles come in three shapes, equilateral triangles, squares, and hexagons, and each polarity for each shape. As the tiles move around, they first form small clusters that are more or less edge-to-edge due to the magnetic attraction. The clusters then agglomerate into larger clusters. Some two-colorable tilings, such as the regular tilings of triangles and squares, form readily. The coloring of the tiles and magnets give these clusters a look similar to some OpArt.

This ceramic sculpture is a fractal tree carried through five generations. With each iteration, the number of branches is tripled. The scaling factor from one generation to the next is the inverse of the square root of 3, approximately 0.577. As more and more branches are added, the top surface begins to display a Sierpinski triangle. The sculpture measures 17" in height.

Star Tessellated Vase
9" x 3-1/4" x 3-1/4"
Ceramics
2013
This tessellated surface of this vase was creating using a laser-cut star-shaped wooden stamp. The placement of the stars created squares in the unstamped clay, resulting in a tessellations of six-pointed stars and squares. I'd like to thank Kevin Lee for laser-cutting the stamp.