2014 Joint Mathematics Meetings
Douglas Burkholder
Artists
Douglas G. Burkholder
Professor of Mathematics
Lenoir-Rhyne University
Hickory, North Carolina, USA
Statement
As a mathematician, I have long enjoyed the artistic beauty and mathematical complexity of fractals. The transformation from a mathematical idea in one's head into a picture generated by the computer is often far different, and often far more interesting than anticipated. In the classroom, fractals are a fun and useful tool for visually illustrating a variety of topics ranging from infinite sequences and series in lower-level courses to abstract metric spaces in analysis. Recently, I have been exploring ways to iterate Borromean Rings while retaining the Brunnian Property. I hope that you enjoy the art and enjoy "seeing the math."
Artworks

The primary sphere in “Spiritual Orbs” consists of three loops tangled together. However, by cutting and removing any one of these loops, as shown in the middle three spheres, the remaining two loops are no longer tangled together. Furthermore, when we consider a single loop, as shown in the top three spheres, each loop is not tangled with itself. Thus, these three loops illustrate the Brunnian Property.
We enhance the geometry and symmetry of the “Spiritual Orbs” with the graceful arches of the Salisbury Cathedral. In the “Spiritual Orbs” we have rings within rings within rings, whereas the Cathedral has arches within arches within arches.
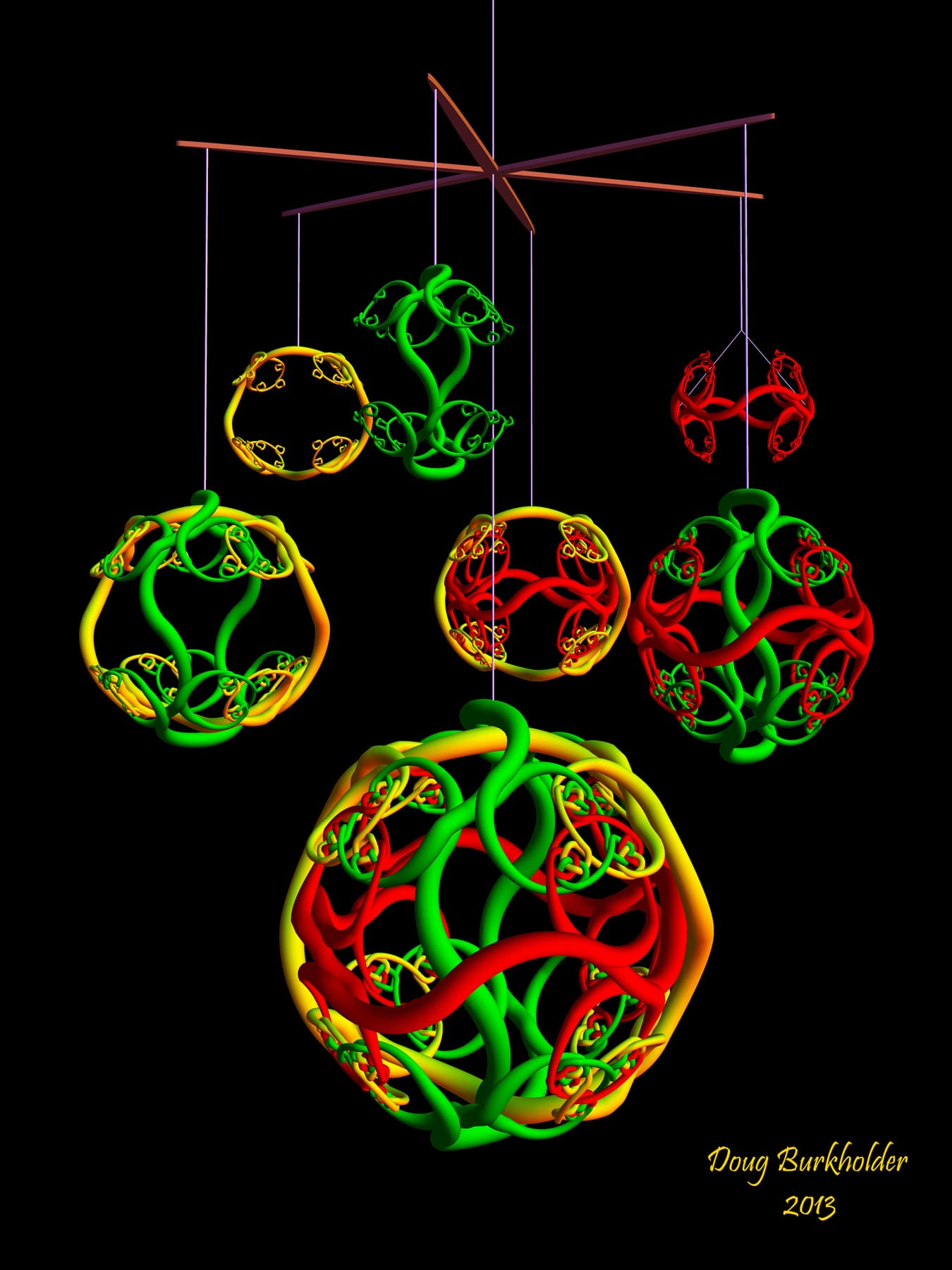
The primary sphere in "A Brunnian Tangle" consists of three loops tangled together. However, by cutting and removing any one of these loops, as shown in the middle three spheres, the remaining two loops are no longer tangled together. Furthermore, when we consider a single loop, as shown in the top three spheres, each loop is not tangled with itself. Thus, these three loops illustrate the Brunnian Property.
The main sphere was created by iterating Borromean Rings. Starting from a spherical representation of the Borromean Rings, planar representations of the Borromean Rings are spliced into each of the eight faces. Twenty-four tiny copies of the Borromean Rings are then spliced into the double intersection regions of the previous Rings.