David A. Reiman
Artists
David A. Reimann
Professor of Mathematics and Computer Science
Albion College
Albion, Michigan, USA
Statement
I am interested in creating patterns that convey messages at multiple levels and scales using a wide variety of mathematical elements and media. I enjoy creating art that uses text to form geometric patterns and geometric patterns that form text. I am also very interested in using tessellations and other modular forms as the basis of interesting 2D patterns and 3D shapes.
Artworks

Studded Walnut
41 x 41 x 41 cm
Walnut veneer and brass fasteners
2015
This form is based on the great rhombicosidodecahedron, an Archimedean solid with 180 edges. The underlying polyhedral edges have been replaced by 4.75 cm squares made from laser-cut paper-backed walnut veneer and connected at their corners with brass split-pin fasteners. The 62 faces (squares, hexagons, and dodecagons) and 120 vertices of the underlying polyhedron are transformed into open negative space. The expansion of linear edges into squares results in a puckered sphere-like shape. The folds and ridges on the surface are evocative of a walnut.

Reptiling Escher
61 x 61 cm
Archival digital print
2015
This work is an homage to the artist M.C. Escher. It is a rendering of a 1943 Escher self-portrait using shapes based on a tessellation of reptiles he created in 1939 and that was featured in his work "Reptiles," also created in 1943. The reptiles in this work vary in thickness proportionally to the underlying image darkness.
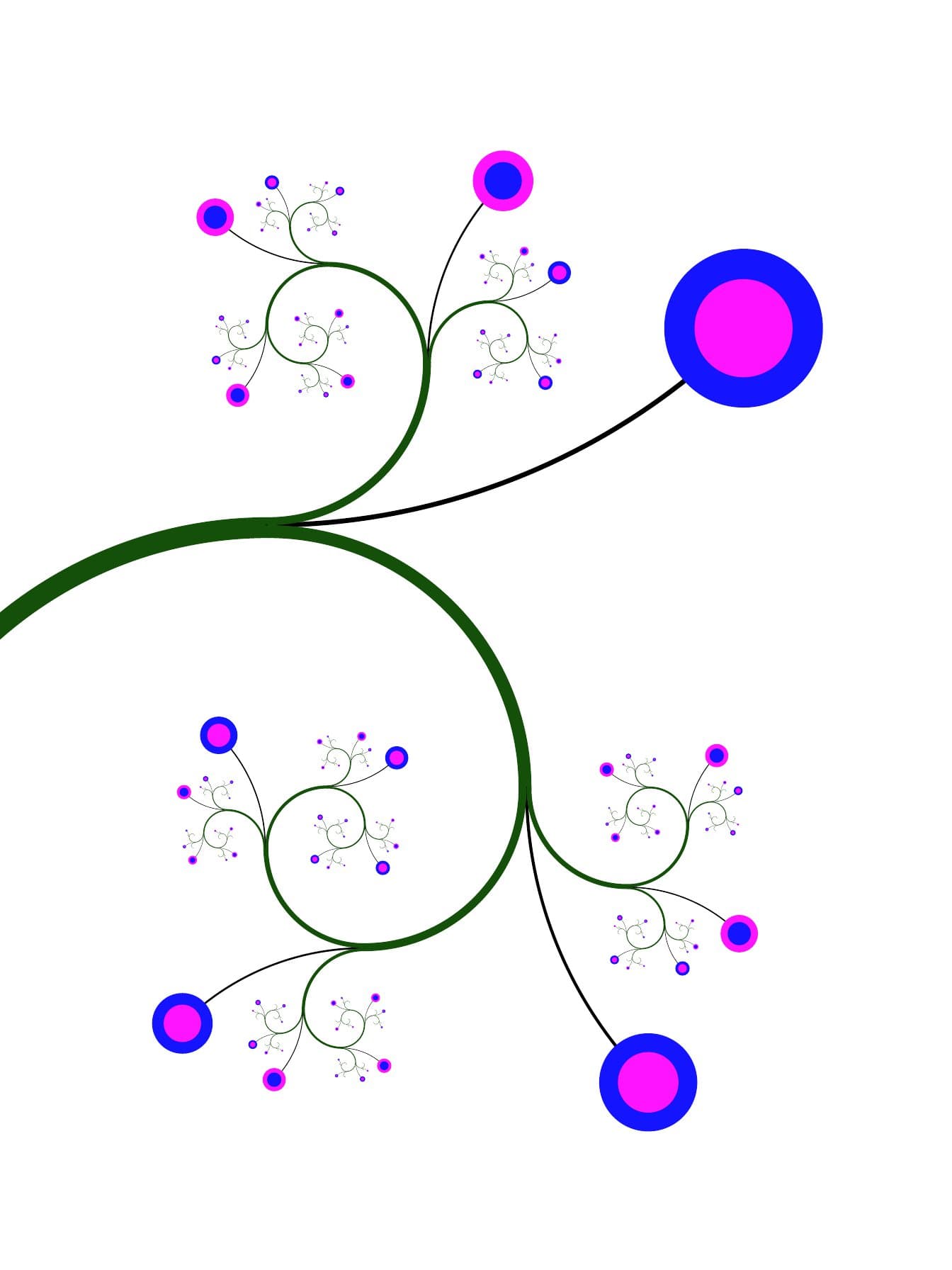
Fibonacci Florescentia
56 x 46 cm
Archival digital print
2015
This work is an abstract representation of a botanical specimen based on a fractal Fibonacci spiral. Individual flowers grow from the bifurcation points and bend toward the smaller fractal component. Flowers are colored depending on the growing angle. Every flower lies along a larger virtual spiral path of similarly colored and bending flowers. The work is made entirely from circular arcs and filled circles.