Simon Ever-Hale
Artists
Simon Ever-Hale
Student
Oberlin College
Oberlin, Ohio, USA
Statement
Half of the algorithmic art I make is based on natural phenomena: trying to imitate and embellish on structures found in nature like tree rings or flocking patterns. The other half comes from mathematical experimentation: asking "What would it look like if...", usually with no idea what the answer might be. I try to pull the two halves towards each other and find forms that are reminiscent of both math and nature. At the core of each of my projects is a mathematical idea, but the development of that project is motivated by the pursuit of the most visually beautiful manifestation of the idea.
Artworks

Cycles
25 x 25 cm
Archival Digital Print
2015
This piece is created entirely using polygons inscribed in a circle, each with all but one sides having the same length. After each iteration, the irregular side grows or shrinks slightly. If the irregular side reaches the same length as the other sides, a new side is added with length zero. If it shrinks to length zero, a new side begins shrinking. By cycling between a set minimum and maximum number of sides and decreasing the radius of the circle over time, a mandala-like pattern is created.
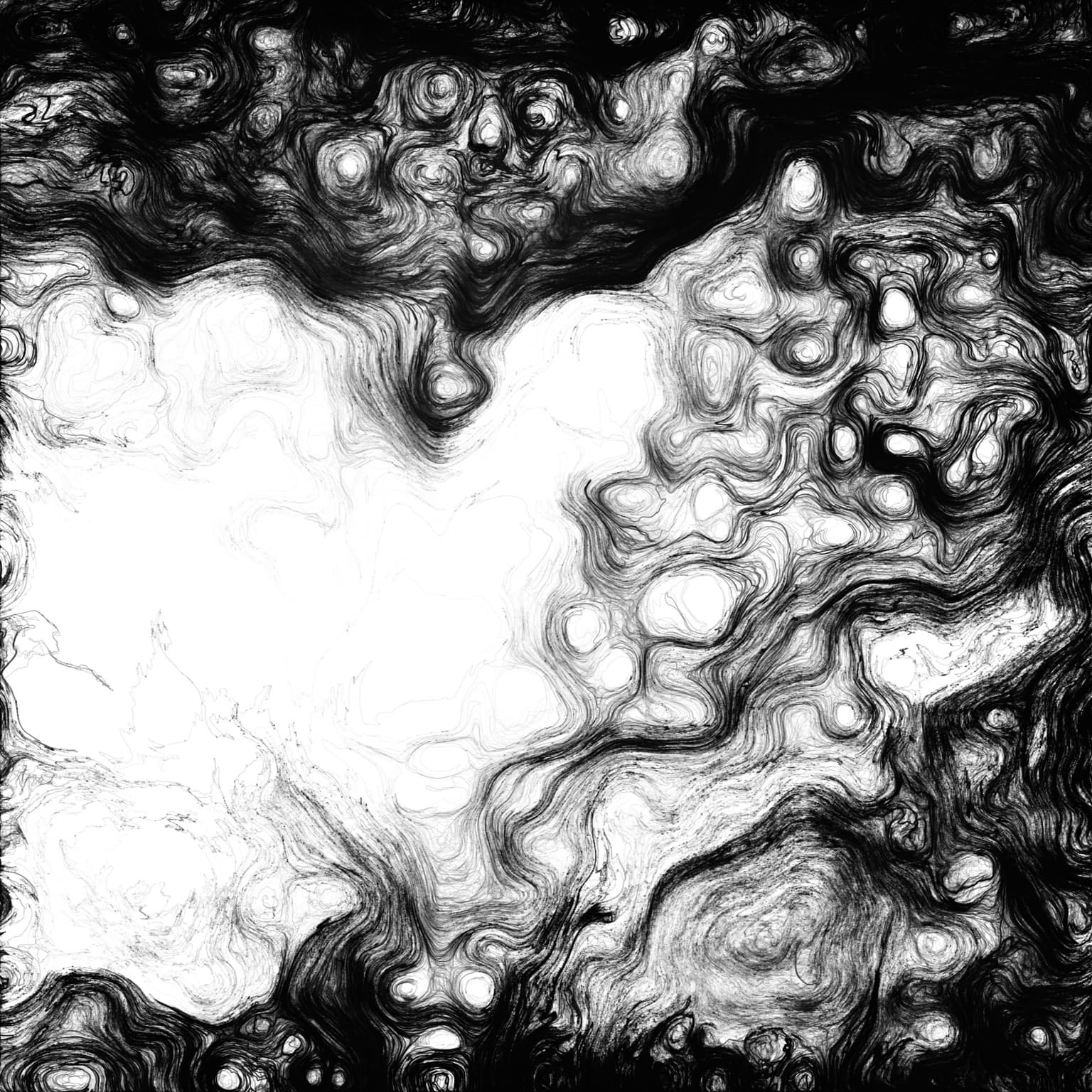
Oil
25 x 25 cm
Archival Digital Print
2016
A random vector field is created, and as thousands of particles flow onto the canvas, outlining the structure of the field, the vector field slowly changes. The changes are a function of the position of another particle as it moves slowly through the vector field, which results in the somewhat erratic, overlapping lines seen here, rather than the smooth curves generated by moving through a static vector field.