2017 Joint Mathematics Meetings
Nick Mendler
Artists
Nick Mendler
Undergraduate Student of Mathematics
University of San Francisco
San Francisco, California, USA
Statement
The artwork below consists of explorations within a family of fractals that have been engineered to exhibit a specific type of connectedness. All fractals are limits, or "canopies" of symmetric binary trees. These trees are defined by two parameters, one that denotes half the angle measure of the spread between branches and a second that sets the ratio between the successive branches. It's possible to narrow this to a one dimensional parameter space by finding a bijection between the angle and ratio parameters that would also force favorable behavior in the canopies. The result has been a fascinating set of fractal curves whose features develop continuously through a wide range of structures.
Artworks
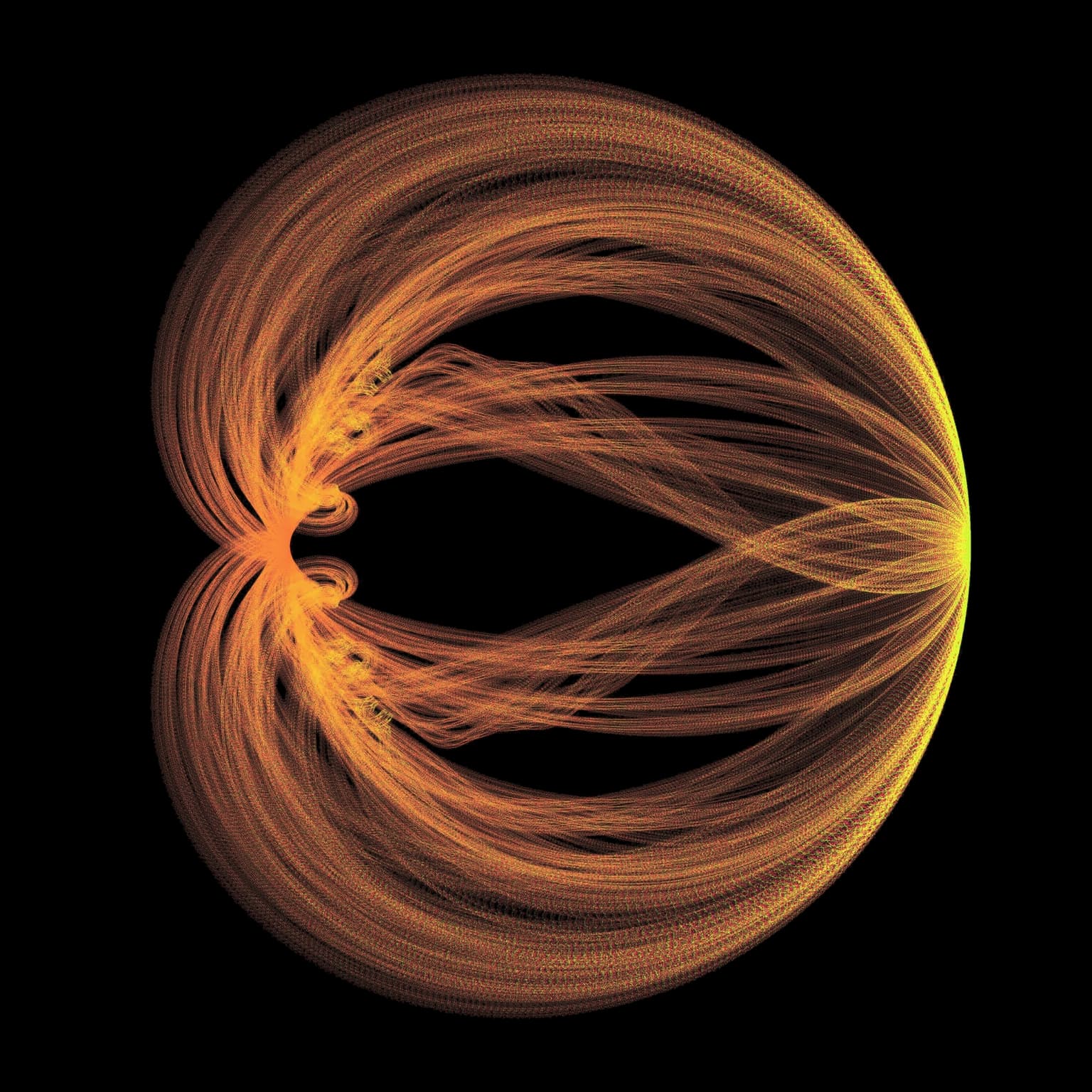
Cardiod Eddies
30 x 30 cm
Digital Print
2016

Woven
20 x 32 cm
Digital Print
2016