Karl Kattchee
Artists
Karl Kattchee
Associate Professor of Mathematics
University of Wisconsin - La Crosse
Wisconsin, USA
Statement
Mathematics can be the subject of art, or it can be part of the process. Sometimes both happen at the same time. I like to experiment, and I have used pencil, pen, pastel, acrylic, paper, cardboard, scanners, cameras, computers, printers, metals, and wood in creating mathematical artwork. This year, my work is based upon de Bruijn sequences of order four, which are binary strings of length 16 whose contiguous length-four substrings form the collection of all possible length-four binary strings.
Artworks
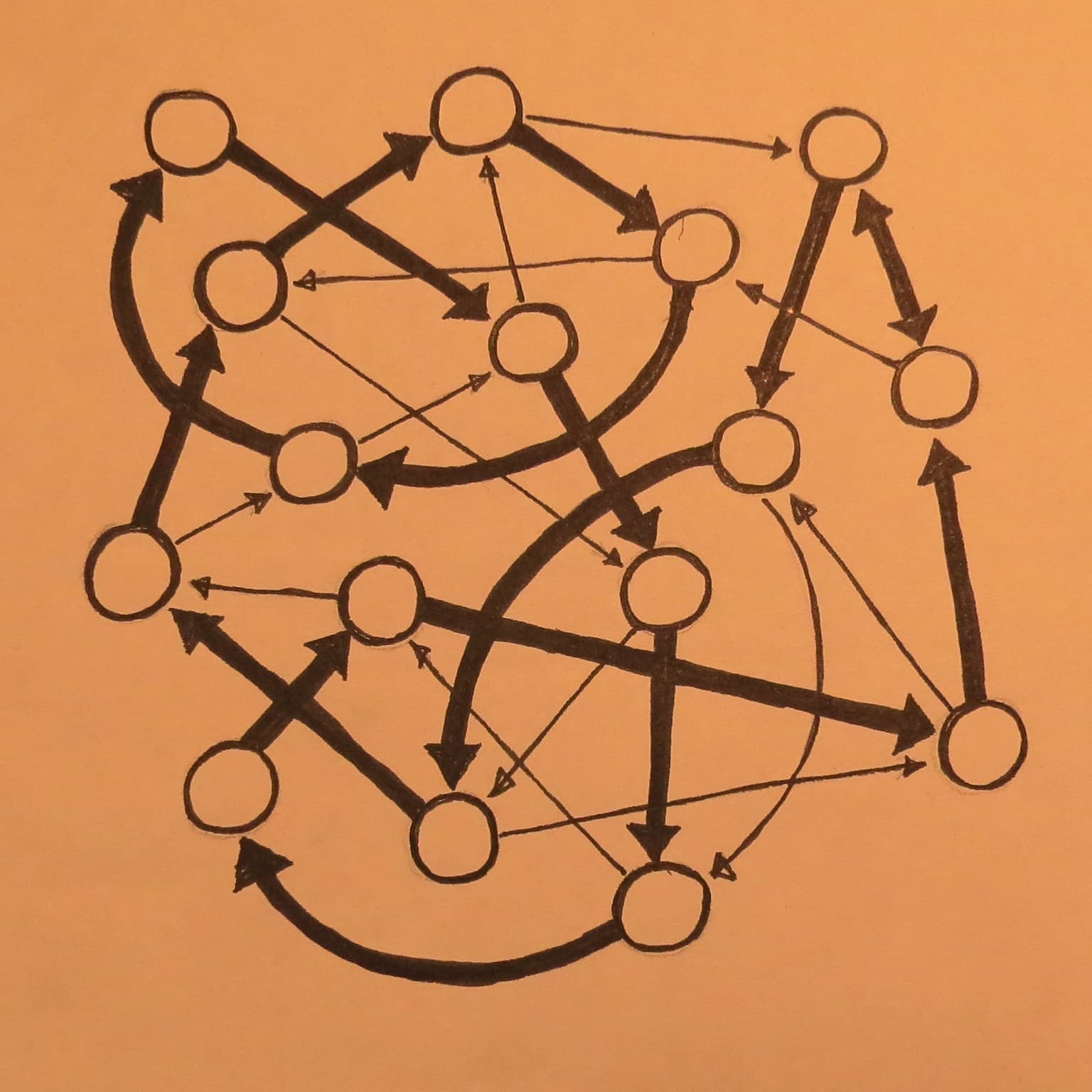
0000111101011001
23 x 23 cm
ink on paper
2018
Without labels on the vertices, it is hard to tell that this is the de Bruijn graph of order four. Each de Bruijn
sequence corresponds to a Hamilton circuit on the de Bruijn graph. The Hamilton circuit which is indicated in the drawing is the one that corresponds to the sequence 000111101011001 (hence the title). With that information, one could recover the vertex labels (length-four substrings).
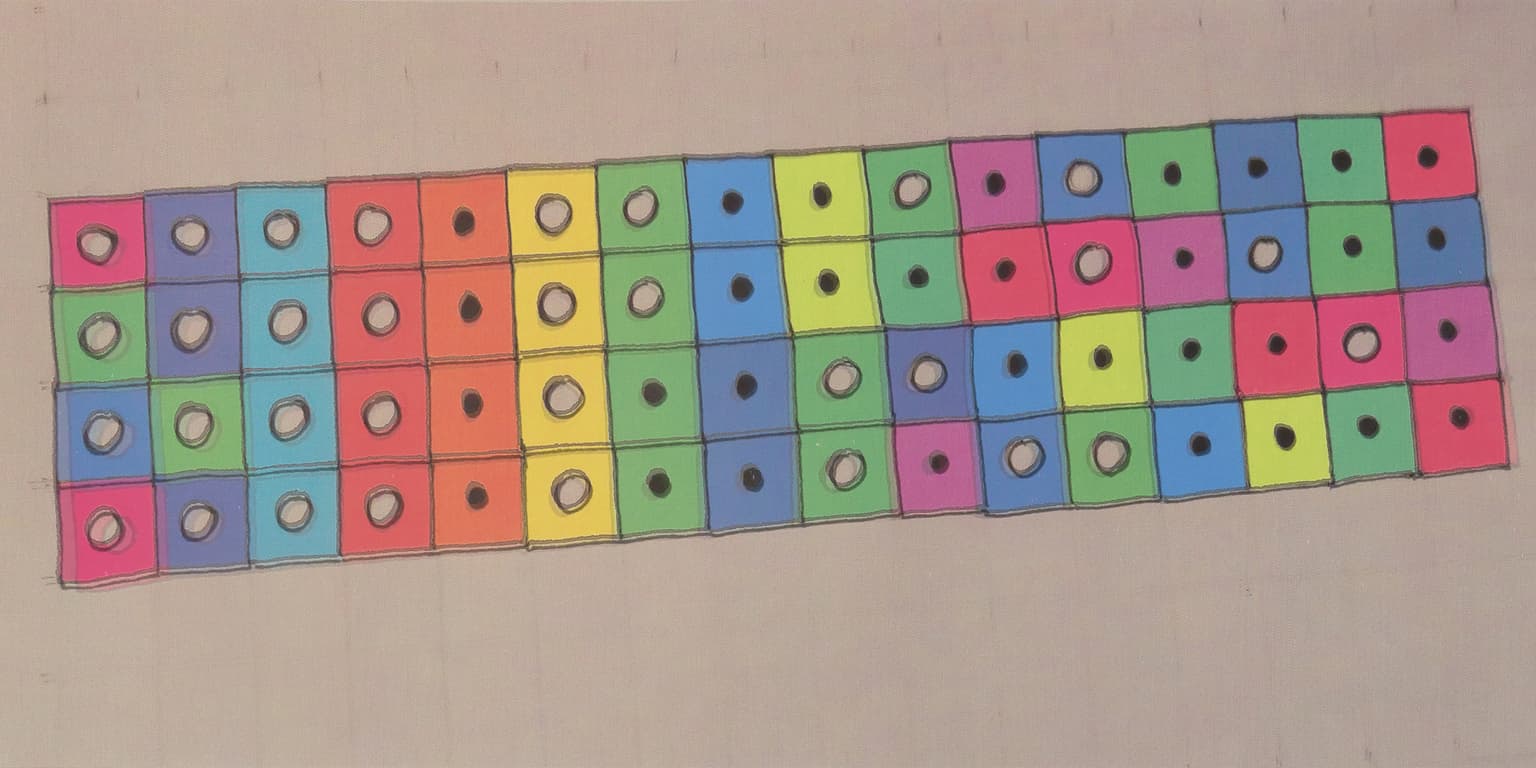
de Bruijn Music
30 x 15 cm
digital print
2018
This is an array of mathematical and visual information. Each row is a representative of one of the four natural equivalence classes of order-four de Bruijn sequences (circle=0 and dot=1). Each de Bruijn sequence can be replaced with a permutation of the numbers 0,1,2,...,15 by converting each length-four substring into its decimal form as a number. The coloring scheme is based on these permutations.