2019 Icerm Illustrating Mathematics
Kathryn Lindsey
Artists
Kathryn Lindsey
Assistant Professor
Department of Mathematics, Boston College
Chestnut Hill, Massachusetts, USA
Statement
My research is in dynamical systems with connections to geometry and topology. I frequently create images, 3D objects, or interactive digital media to help gain intuition about the mathematical objects I study.
Artworks

A variant of the Alexander horned sphere
20 x 25 cm
digital print on metal
2007
I created this image of a variant of the Alexander horned sphere while taking a course called "the Art and Science of Computer Graphics," taught by Duane Bailey, as an undergraduate at Williams College. The 3D set depicted here in gold is homotopic to a solid ball in 3-space; one might imagine continuously retracting the "arms" of the object and watching it shrink down to become a round ball. The complement of this set in Euclidean 3-space, however, has a much more complicated topological structure than the complement of a geometrically round ball.
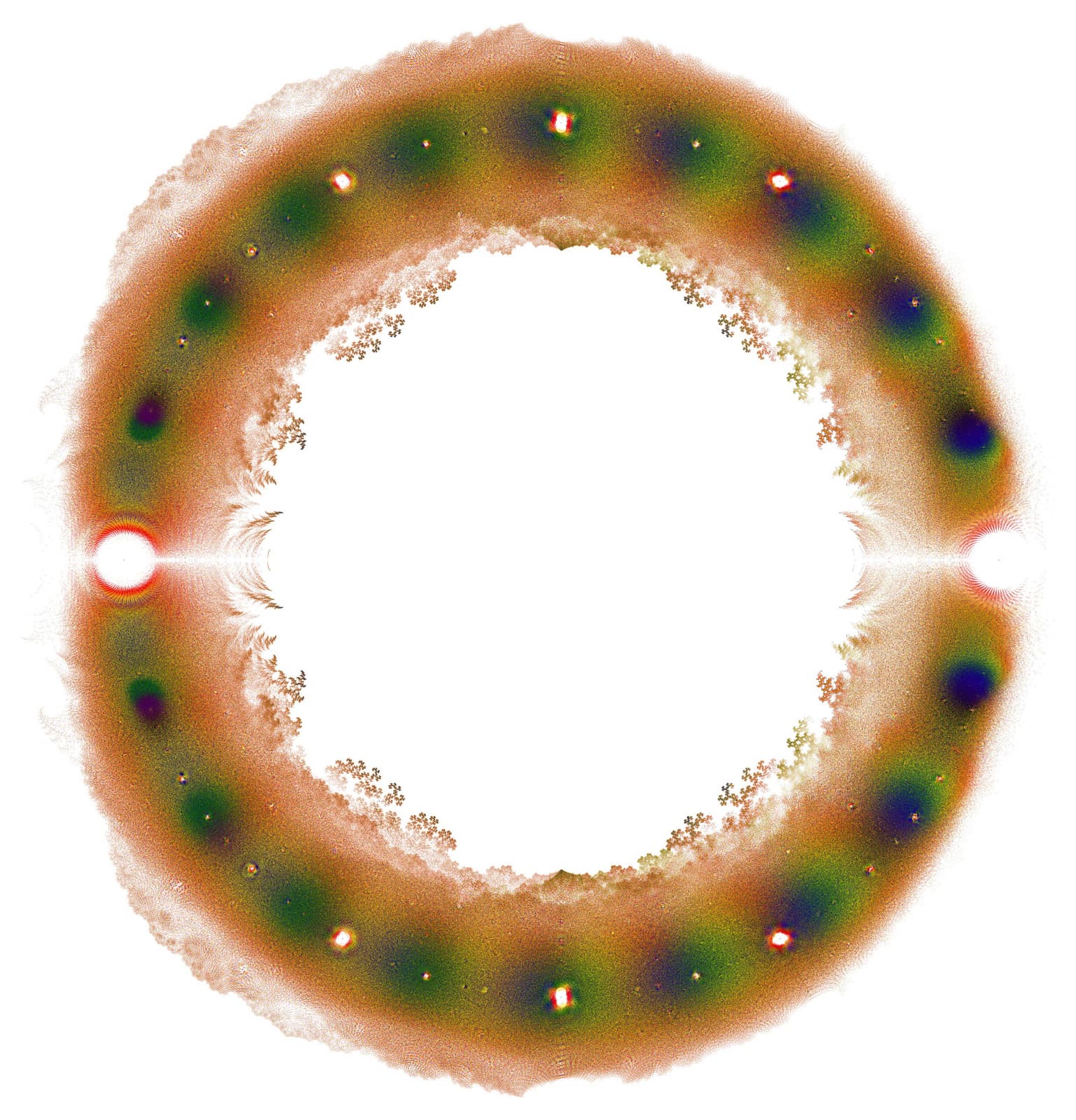
Ring of fire from PCF interval self-maps
76 x 76 cm
digital print on canvas
2017
Joint with Harrison Bray, Diana Davis, and Chenxi Wu. This plot was created using Mathematica at an AMS Mathematics Research Community program on "Dynamical Systems: Smooth, Symbolic & Measurable" as part of our joint research on the growth rates of post-critically finite interval self-maps. It is a plot of all Galois conjugates of growth rates of post-critically periodic generalized beta transformations with a growth rate in [1,2] and critical period at most 22, colored according to the critical period. The project culminated in our research paper, "The Shape of Thurston's Master Teapot" (2019, preprint on ArXiv.org).

Joint with Harrison Bray, Diana Davis and Chenxi Wu. As part of our research on Thurston's Master Teapot, we created this video to try to gain insight into the geometrical and topological properties of that set. Each frame of the video shows a 2D "slice" of the 3D set; a slice consists of Galois conjugates of growth rates of unimodal, super-attracting interval self-maps with a growth rate in a very small interval. Careful scrutiny of the video may lead one to conjecture that that points outside the unit circle (shown in white) vary continuously, while the points inside the unit circle "approximately persist"; our joint paper "The Shape of Thurston's Master Teapot" (2018) proves this result.