2019 Joint Mathematics Meetings
Margaret Kepner
Artists
Margaret Kepner
Independent Artist
Washington, District of Columbia, USA
Statement
I enjoy exploring the possibilities for conveying ideas in new ways, primarily visually. I have a background in mathematics, which provides me with a never-ending supply of subject matter. My lifelong interest in art gives me a vocabulary and references to utilize in my work. I enjoy expressing mathematical concepts through attributes such as color, geometric forms, and patterns. One topic I have explored recently is integer sequences -- their distributions, rhythms, and overlaps. When these sequences are displayed in different formats, interesting relationships are revealed.
Artworks

Dueling Spirals 101
40 x 68 cm
Archival Inkjet Print
2018
A square spiral structure provides the basis for this piece. Each of the two spirals grows outward (from a central square representing “one”) in a sequence of trapezoids culminating in the 101st one at the top. In the left-hand spiral, regions corresponding to prime numbers are colored cyan, while those belonging to other number sequences (happy, triangular, and Fibonacci) are assigned the colors magenta, yellow, and transparent white. Integers that are associated with more than one sequence result in mixed hues. On the right-hand side, the direction of the spiraling trapezoids is reversed, and a different selection of integer sequences is represented. These are the lucky, harshad, generalized pentagonal, and Lucas numbers.
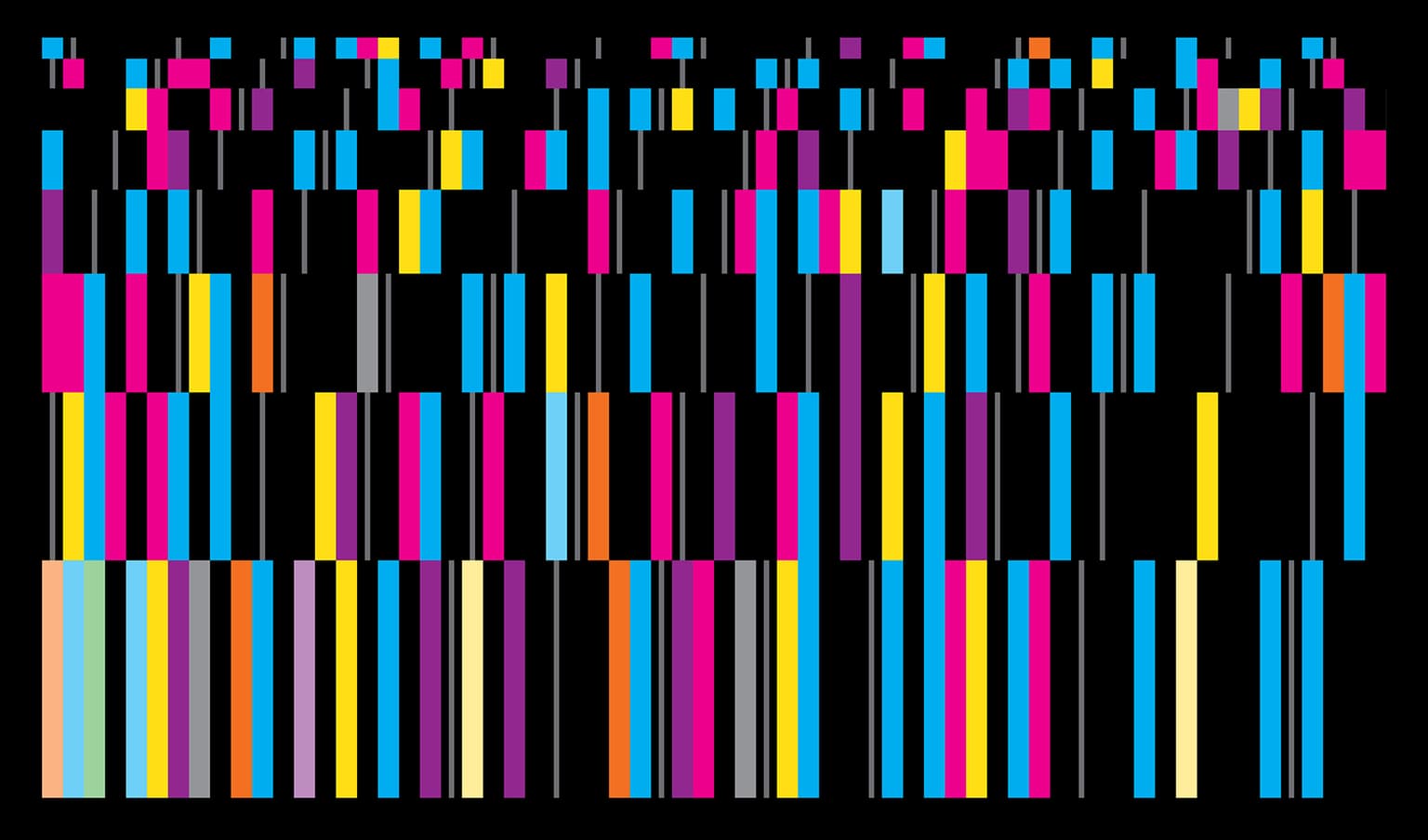
Sequential Layers 512
40 x 60 cm
Archival Inkjet Print
2018
In this work, several integer sequences are shown in a stacked number-line format. The bottom row is composed of vertical bars corresponding to the numbers from 1 to 64. This second row begins with 65 and ends with 128. This logic continues for each row, ending with 512 in the upper right. Row heights are scaled for compactness. A bar is colored cyan if it is a prime, magenta if it is a happy number, and yellow if it is a triangular number; otherwise it is black. If an integer belongs to more than one sequence, the colors are blended. A white scrim is added to indicate Fibonacci numbers, and thin gray lines provide a reference grid. The rhythms and juxtapositions that are produced suggest a color-coded musical score - a form of visual jazz.