2020 Joint Mathematics Meetings

Skylar Cheung

Artists

Skylar Cheung

Visual Artist

Political Science Department, University of Toronto

Toronto, Ontario, Canada

skylar.cheung@mail.utoronto.ca

http://cherylskylar.com

Statement

My name is Skylar, and I am a visual artist based in Toronto. I usually rely on mathematical formulae to build visual guides for other oil paintings. This time around, I wanted to try my hand at using visual arts to put math at the forefront. I hope that in using a variety of materials and a spectrum of basic colors, viewers will have a clear understanding of which mathematical ideas each piece represents. Though I like paints and political science (my declared academic discipline) plenty, I do like to exercise my mind with logic puzzles found online. I am also interested in exploring impossible shapes in design making. Ultimately, I hope that my visual art will eliminate the panic so many people associate with mathematics.

Artworks

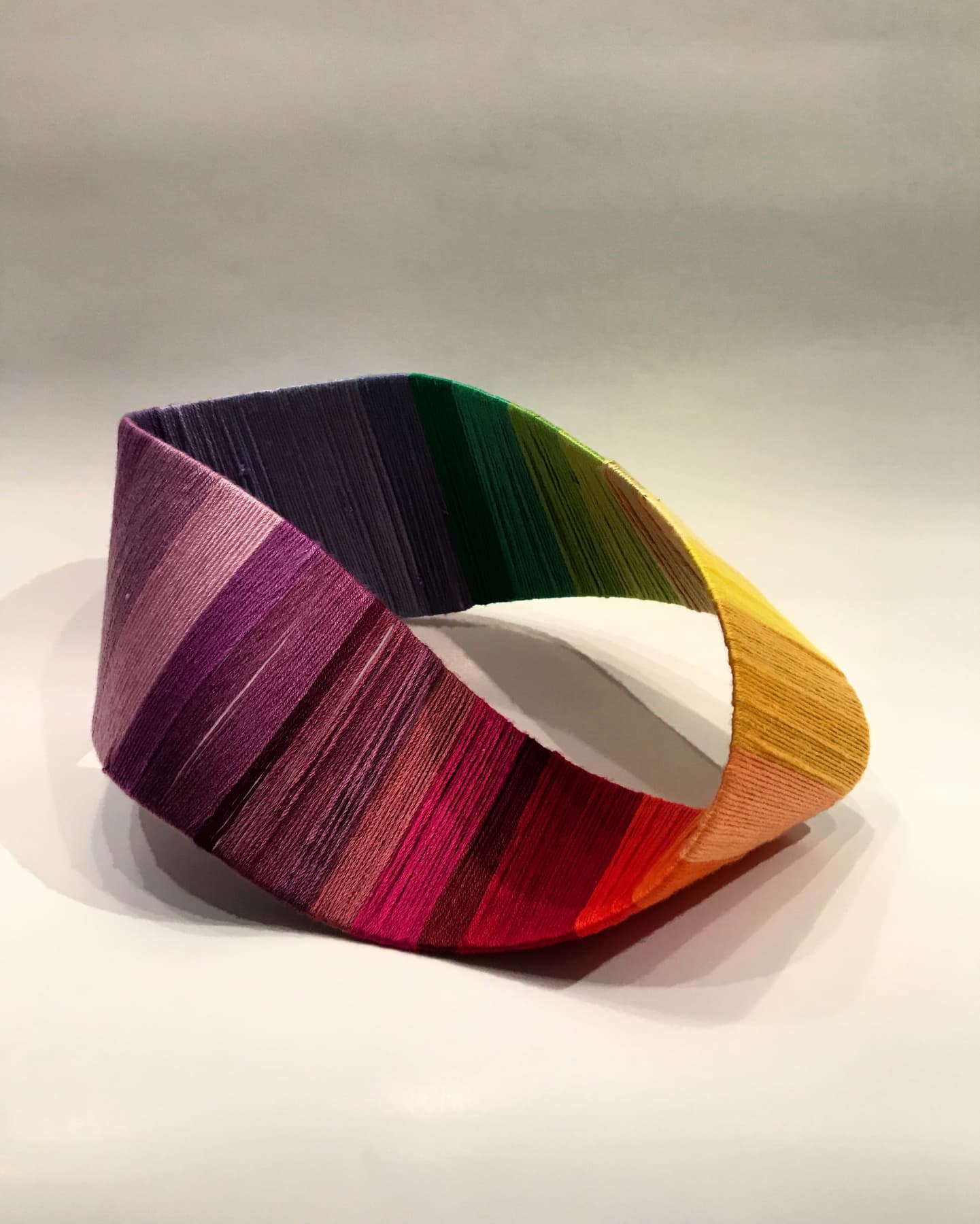
Image for entry 'Infinite Loop, Thread on Mobius Frame'

Infinite Loop, Thread on Mobius Frame

13 x 30 x 25 cm

Thread on cardstock frame

2019

One can obtain an orientable torus by deforming string wrapped around the non-orientable Mobius strip.Though the torus and the Mobius strip have the same fundamental groups, they are not homotopy equivalent (there is no continuous way to turn one surface into another). This work demonstrates a simple example of a broader topological question: what are the properties of a surface obtained by wrapping-string around a “parent” object and uniting the strands? Consider two objects A and B. Wrap string around their inner and outer surfaces, and glue the loops of the string together in order to get corresponding surfaces A* and B*. If you can pull and push (without tearing!) A* into B*, then A and B are homotopy equivalent. Can you prove it?