2021 Joint Mathematics Meetings
David Lowry-Duda
Artists
David Lowry-Duda
Senior Research Scientist
ICERM
Boston, MA
Statement
I am drawn to images with a sense of randomness, but which I know are exact and determined. In my research, I often study how number theoretic objects behave in comparison to randomness. There is a tug of war. In my art, I try to capture this conflict, both the structure and the disarray. Most of my work is closely related to objects in my research. Modular forms, algebraic varieties, and lattice points serve as inspiration and lurk closely behind each piece.
Artworks
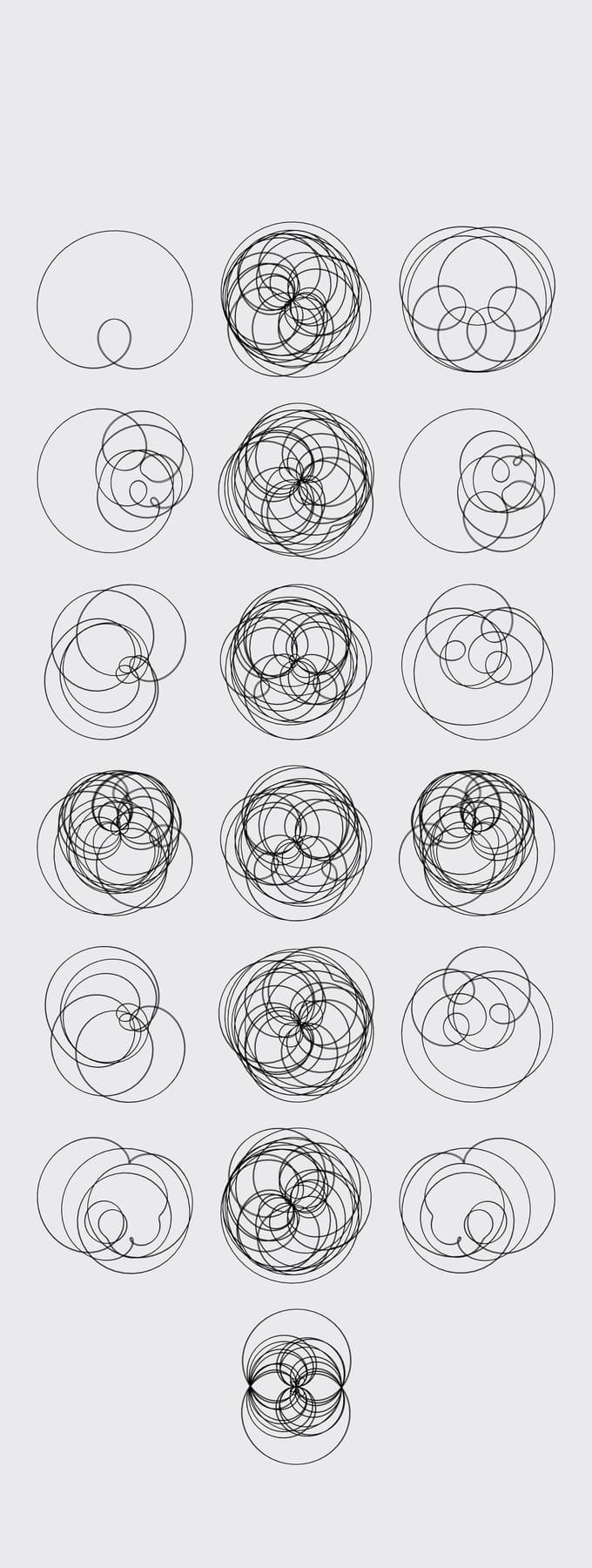
Dirichlet characters mod 33
47 x 18 cm
Digital print
2020
This composition features the 19 nontrivial Dirichlet characters mod 33. (The trivial Dirichlet character would consist of a single point). We typically think of Dirichlet characters as discrete group homomorphisms from a finite group, but in analytic number theory it is often convenient to interpolate the character to a map from the real numbers. Identifying these characters with their interpolations and plotting the images of the real line yields the collection of images here. Each character takes values on the unit circle and at the origin, which is why we can recognize underlying circles. Some of the characters are unique, while others form sets that transform into each other through a symmetry (and which lie in the same Galois orbit).

Rational points on the circle
60 x 60 cm
Digial print
2020
This composition is based on visualizing rational points on the unit circle. The challenge in visualizing these rational points is that they all lie on the circumference, and that hides the underlying structure. Here, each point is plotted at the correct angle, but at a radius equal to the largest denominator (what an arithmetic geometer might call naive height) of the coordinates of that point. Close examination shows the 4 points (1,0), (0, 1), (-1, 0), and (0, -1) near the center, and then four notable rays without rational points in the cardinal directions. Trying to understand this avoidance first led me towards this picture. Countless parabolas manifest among the points, hinting at height-preserving projections to conics.