Merrill Lessley

Statement

In my interdisciplinary research and creative work, I create laser images in motion that represent specific mathematical curves (epicycloids, hypocycloids, roses, epitrochoids, hypotrochoids, and other special sine/cosine cases). These images are created by using a computer-controlled laser projection system that I have designed and built. Graphing such curves in multiple laser colors produces a wide variety of images that are really quite beautiful. Unlike drawing them on paper, however, projecting such curves with a laser, or several lasers, poses a particularly challenging problem: while a laser is often referred to as a kind of "pencil" in light, it can only be used to generate a complete picture by moving its projected "dot" rapidly and repeatedly over a reflective surface. The images I create must be scanned at rates between 15 and 2000 times per second. My primary goal is to create computerized tools that can be utilized by laser artists throughout the world.

Artworks

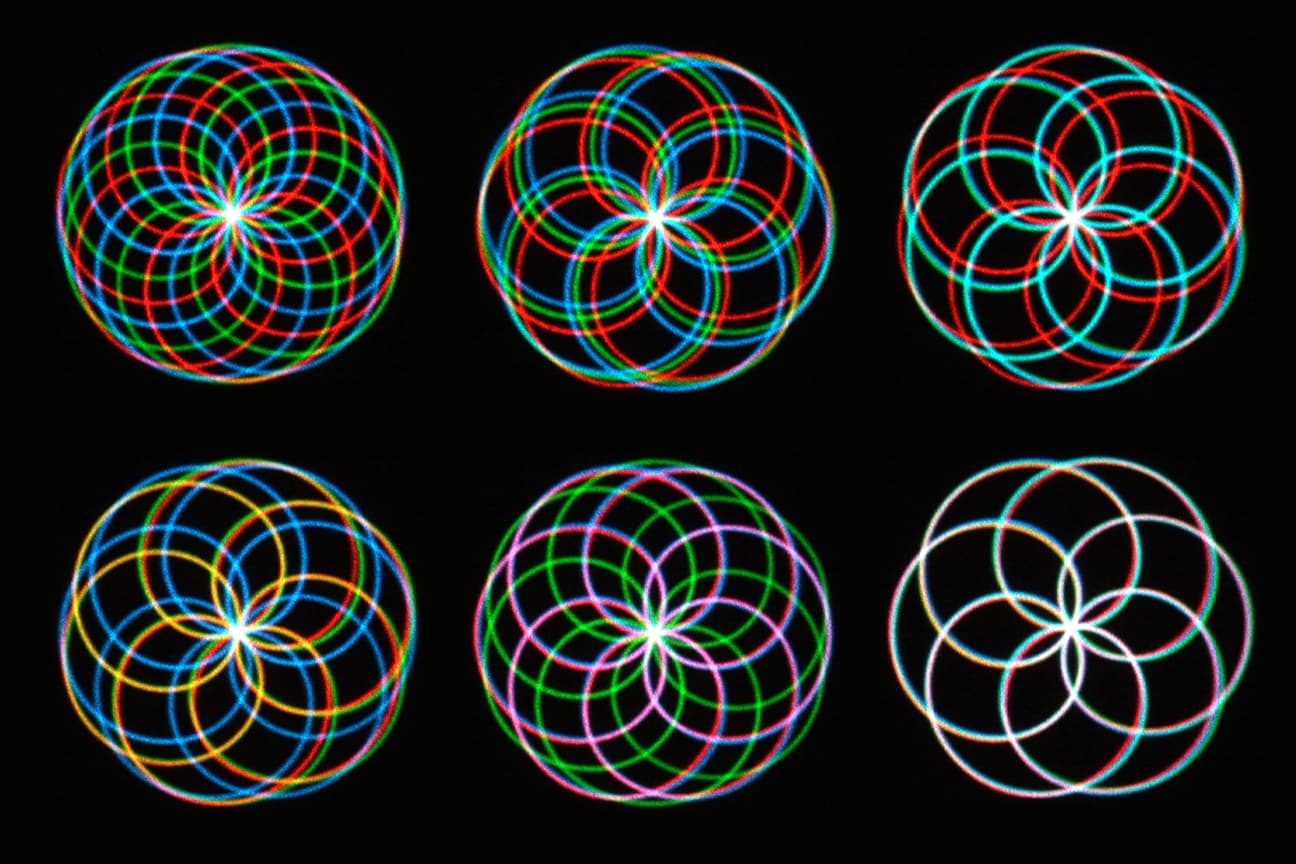
“Laser Rose” was constructed by applying mixtures of sine and cosine signals to three lasers programmed to scan rapidly on “X” and “Y” axis lines moving rapidly in various directions. These images represent a sequence of photos extracted from a high-resolution video recording of the lasers scanning a six petal rose curve. Creating the art required a mathematical approach similar to the graphing of any hypotrochoid curve. However, since we use base and trace oscillators to form images, traditional parametric equations were modified to accommodate the “dynamic” scanning process. Revised equations considered both base and trace frequencies: x = (a-b) cos(ωt) + h cos(((a-b)/b) ωt); y = (a-b) sin(ωt) + h sin(((a-b)/b) ωt). Also, ω = 2πf, where the base frequency f is the number of times per second that the base oscillator completes a cycle. Since the rose curve is a special case of the hypotrochoid function, a = (2n) h/(n+1), b = (n-1)/(n+1) h, where n is the number of petals.