2011 Joint Mathematics Meetings
Tobias Friedrich
Artists
Tobias Friedrich
Research associate
Max Planck Institute for Informatics
Saarbrücken, Germany
Statement
I am a researcher at the Max Planck Institute for Informatics in Saarbrücken, Germany. My research interest are probabilistic methods and quasirandomness. Some structures I have examined mathematically also give rise to pictures that exhibit surprising beauty.
Artworks
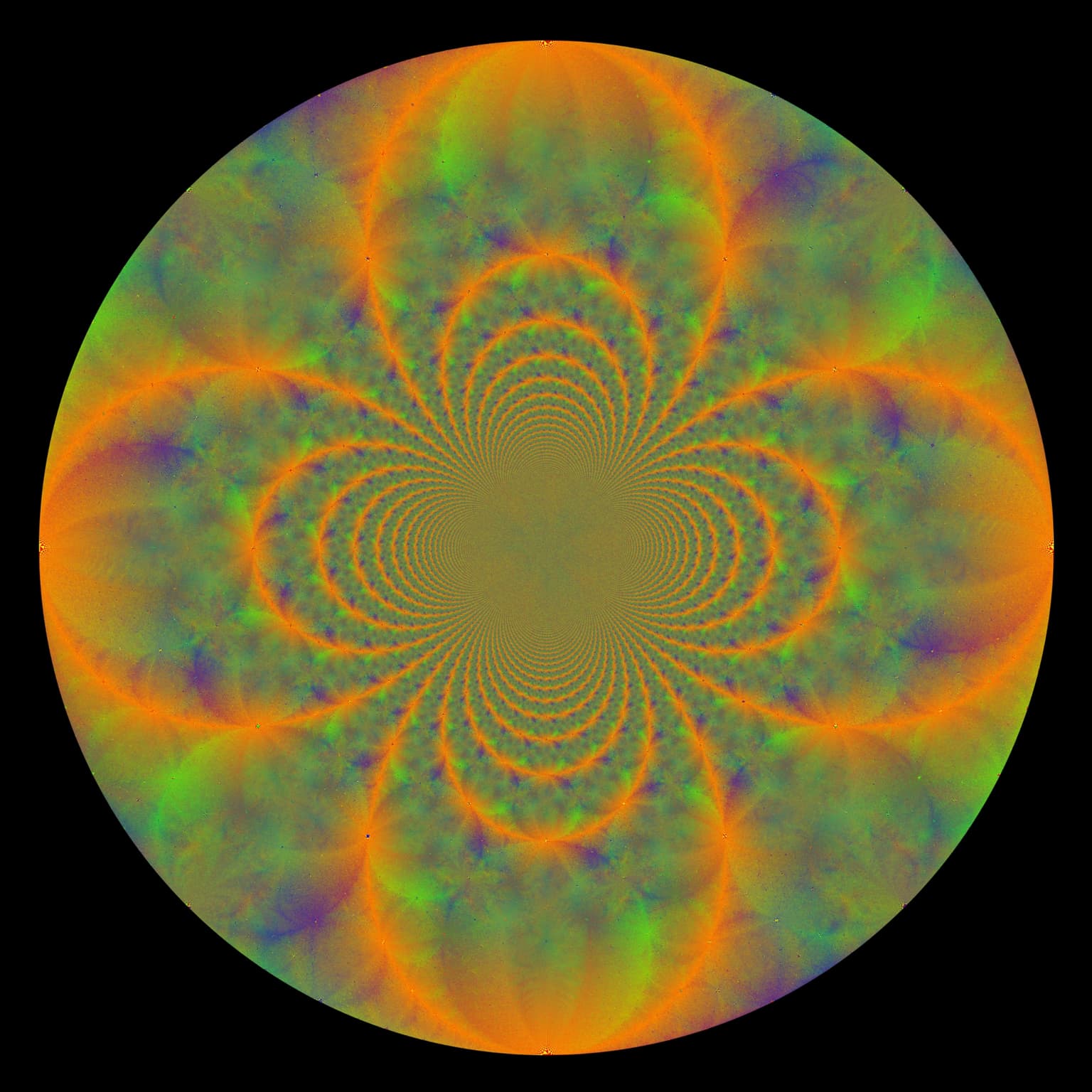
Quasirandom Aggregation
20" x 20"
Digital print on glossy paper
2010
Given an arbitrary graph, a random walk of a particle is a path that begins at a given starting point and chooses the next node with equal probability out of the set of its current neighbors. Around 2000, Jim Propp invented a quasirandom analogue of random walk. Instead of distributing particles to randomly chosen neighbors, it deterministically serves the neighbors in a fixed order by associating to each vertex a "rotor" pointing to each of its neighbors in succession. The picture shows what happens when one billion particles are placed at the origin and each one runs until it reaches an unoccupied vertex. Black pixels denotes cells that never get visited by a particle; for the other cells, the color of the pixel indicates in which direction the rotor points at the end of the process. More information can be found at http://rotor-router.mpi-inf.mpg.de.