2012 Joint Mathematics Meetings
Robert Fathauer
Artists
Robert Fathauer
Owner
Tessellations
Apache Junction, Arizona, USA
Statement
I’m fascinated by beautiful and complex forms both in mathematics and in the natural world. I’m particularly intrigued by complexity that possesses infinite detail, but also underlying order. Combining mathematics with artistic creativity allows me to explore and express these ideas in unique images.
Artworks
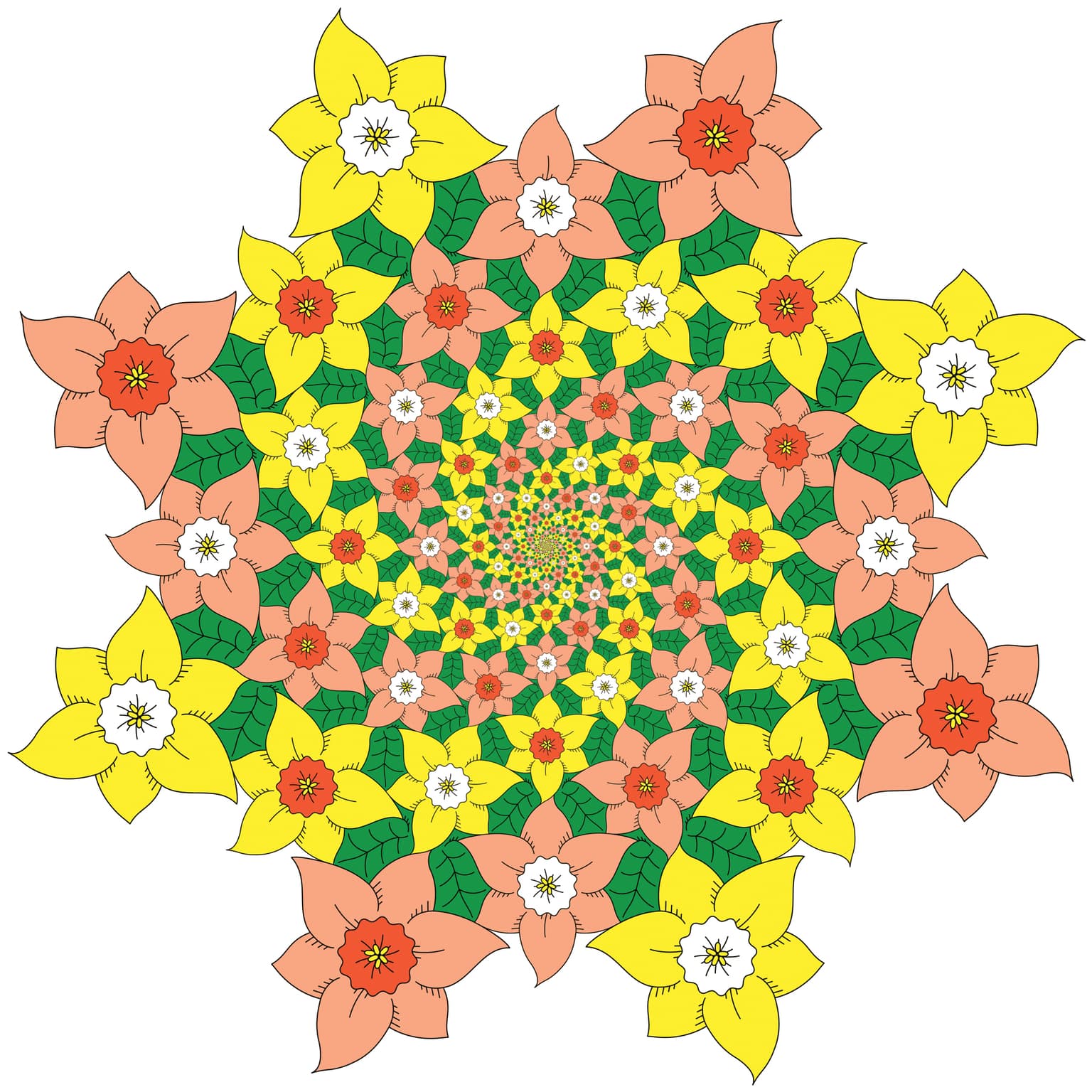
Spiraling Flowers
16" x 16"
Archival inkjet print
2011
Tessellated flowers and leaves are arranged in a pattern with eight-fold rotational symmetry (four-fold if color is considered). Selective coloring of the outer and inner portions of the flowers brings out sets of counter-rotating spirals.

Fractal Tessellation of Spirals
16" x 16"
Archival inkjet print
2011
This artwork is based on a fractal tessellation of kite-shaped tiles I discovered several years ago. Grouping of the kite-shaped tiles into spirals allowed a fractal tessellation to be created in which two colors were sufficient to ensure that no two adjacent tiles have the same color. All of the spirals in the print have the same shape (more precisely, they are all similar in the Euclidean plane).