2013 Bridges Conference Short Movie Festival
Jarke J. van Wijk
Filmmakers
Jarke J. van Wijk
Professor of Visualization
Dept. Mathematics and Computer Science, Eindhoven University of Technology
Netherlands
Statement
My focus is on visualization, the use of interactive computer graphics to explore large amounts of data as well as to understand mathematical concepts. I try to develop new visual metaphors and explore the design space. Given a problem, what are the rules of the game, and what happens if we explore the limits? How can we translate the fascinating concepts and challenges into understandable and interesting images, animations, and applications?
Films
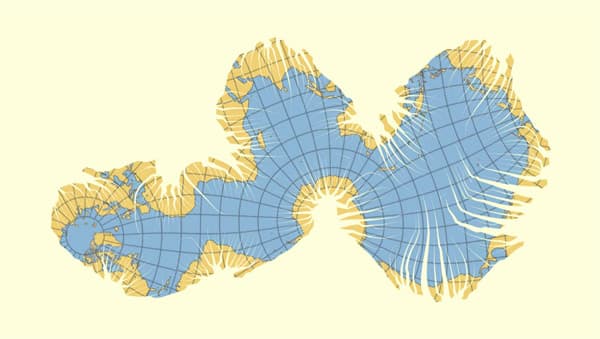
Myriahedral Projections
00:02:00
2010
Mapping the earth is a classic problem. Distortion seems inevitable, and many mathematicians, cartographers, artists and designers have proposed projection methods. However, if we do not care about interrupts, maps that are almost free of distortion can be obtained. Or, in other words, it is easy to flatten an orange peel, isn't it?
The method is based on projecting the globe on a myriahedron, a polyhedron with many facets. Next, this myriahedron is unfolded, giving an almost distortion free projection. By selecting the way the facets are placed and deciding where to cut and fold many variations can be produced. The examples shown in the video are inspired by classical maps; projections on subdivided Platonic solids; the use of meshes aligned by continents; and torn meshes.