Jean Constant

Statement

Often artists use art to abstract their immediate environment. In reaching for mathematics, the most abstract universal expression of human consciousness, I found a limitless source of inspiration that helps me map out and develop a visual discourse in a larger, more familiar cultural context. The digital technology has expanded greatly the scope and effectiveness of visual expression. It has helped me deepen my interest in exploring abstract concepts and bring to life forms and circumstances that surround us and that the mathematical language has so beautifully mapped out for us.

Artworks

From the “shortest route problem” model used by Evan L. Porteus to illustrate the recursive method of calculation to solve problems when elements of uncertainty or chance are introduced. In this image (3 different sizes of the same table) the squares represent the decision nodes, the spheres the chance nodes. I slightly enlarged node #21 (or one) to point to the minimum expected distance. A slight additional random after-effect can also be noticed from the juxtaposition of white sphere/black polygons, when moving the eye rapidly across the surface of the composition.

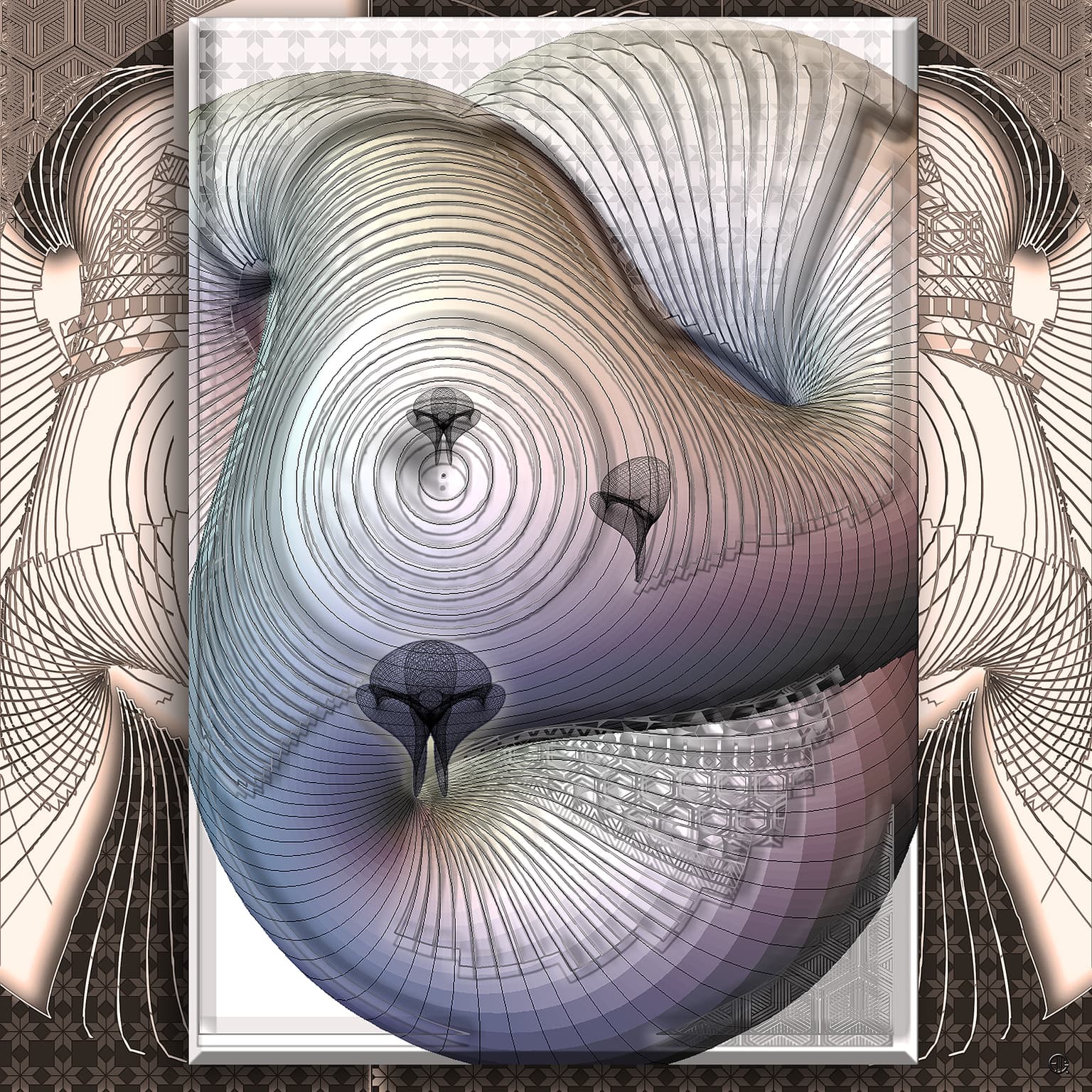
A Boy's surface is an immersion of the real projective plane in 3-dimensional space. It was discovered by Werner Boy in 1901. This surface is a non-orientable surface for which it is impossible to make a consistent choice of "front" and "back”. For artists, it makes an interesting challenge to translate in visual term such an abstract mathematical concept.

The Julia set is named after the French mathematician Gaston Julia. It consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated function values. The image is created by mapping each pixel to a rectangular region of the complex plane and by coloring the point by how fast it diverges to infinity.