Teresa Downard
Artists
Teresa Downard
Mathematics Instructor
Mathematics Department, Western Washington University
Bellingham, Washington, USA
Statement
As an artist I am exploring the parallels between visual and mathematical abstraction, symmetry, and symbolism that tie into my mathematical interests. To illustrate relationships I like to use analogy with human experience, natural textures, and the juxtaposition of colors. I typically paint in acrylics and oils, and also enjoy doing ink and pencil compositions.
Artworks

Reflections
8.5 x 11 in
acrylic on board
2013
This piece began as a depiction of O(3), showing rotations of an object about different lines of symmetry to represent SO(3) and its reflection. Setting the backdrop with the idea of space and fluidity, and setting down the lines of symmetry, the piece seemed complete already. Disappointed that the more sophisticated mathematical ideas would not be shown explicitly but unwilling to clutter it with more content, I've started to think about it as one of those pauses you take to appreciate a simple but elegant mathematical idea that may have hidden depth.
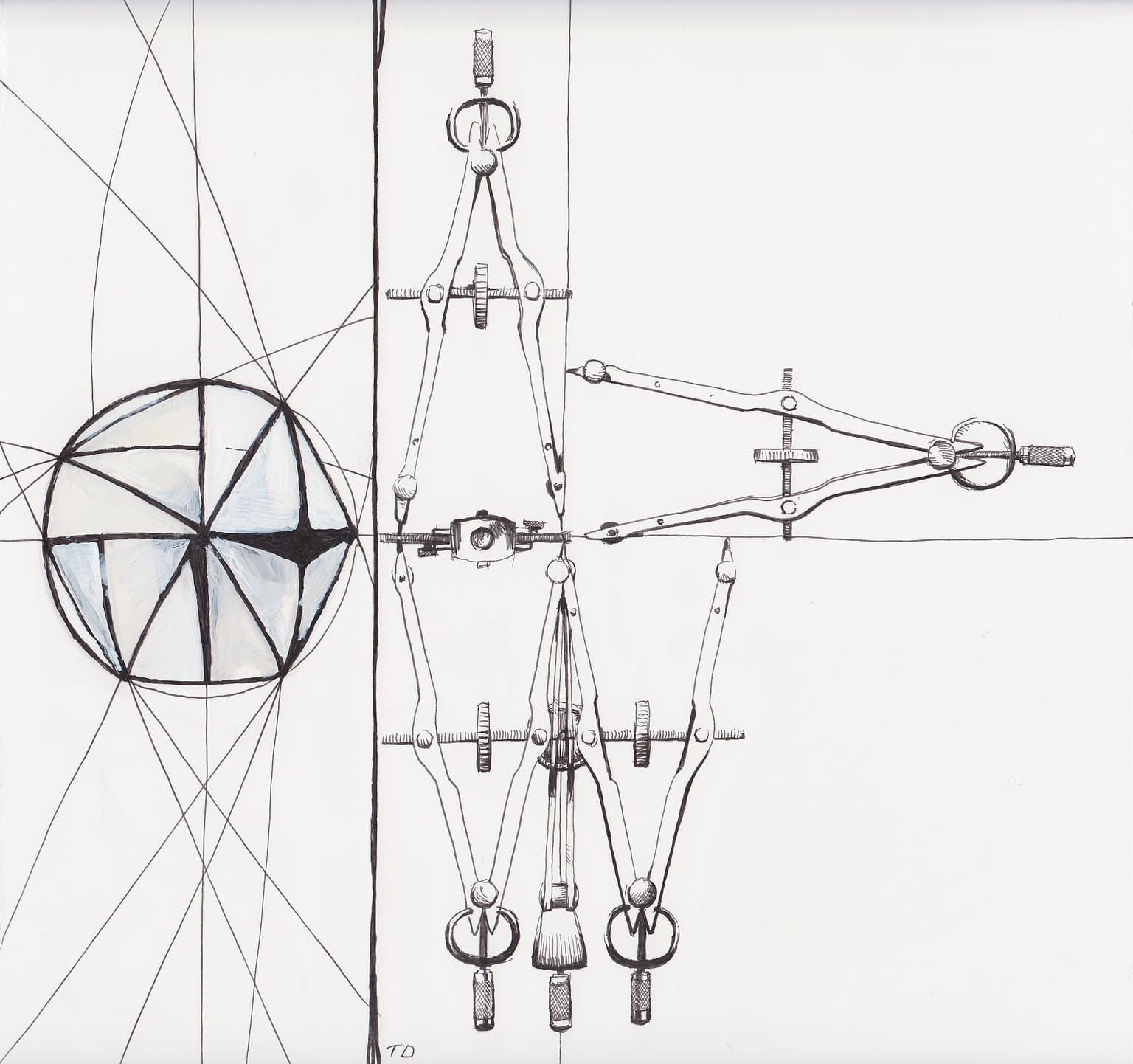
Reflections II
22 x 22 cm
technical pen and acrylic on Bristol paper
2014
The orthogonal group of order 3 is made up of two disjoint parts: the set of all rotational symmetries and its reflection. This is a second attempt to portray this idea. There is a series of rotations of the compass about three orthogonal lines in space and an abstract reflection, hinting at the geometric and algebraic at play in the study of these groups and others like them in Lie theory.