2014 Joint Mathematics Meetings
Ellie Baker
Artists
Ellie Baker
Artist and Computer Scientist
Cambridge, Massachusetts, USA
Statement
For me, creating visual art reflects a quest for deeper understanding--of science, mathematics, society, or self--and a wish to share the quest. This piece is an outgrowth of an extended research project with Susan Goldstine on applications of mathematics to bead crochet. Bead crochet’s spiral structure creates constraints that make it especially challenging to produce symmetric designs, but its stretchiness and flexibility give it a topological flavor that lends itself nicely to torus knot explorations. In our forthcoming book, “Crafting Conundrums: Puzzles and Patterns for the Bead Crochet Artist” (AK Peters/CRC Press), we devote a chapter to torus knots, going from thought experiments to practical bead crochet constructions.
Artworks
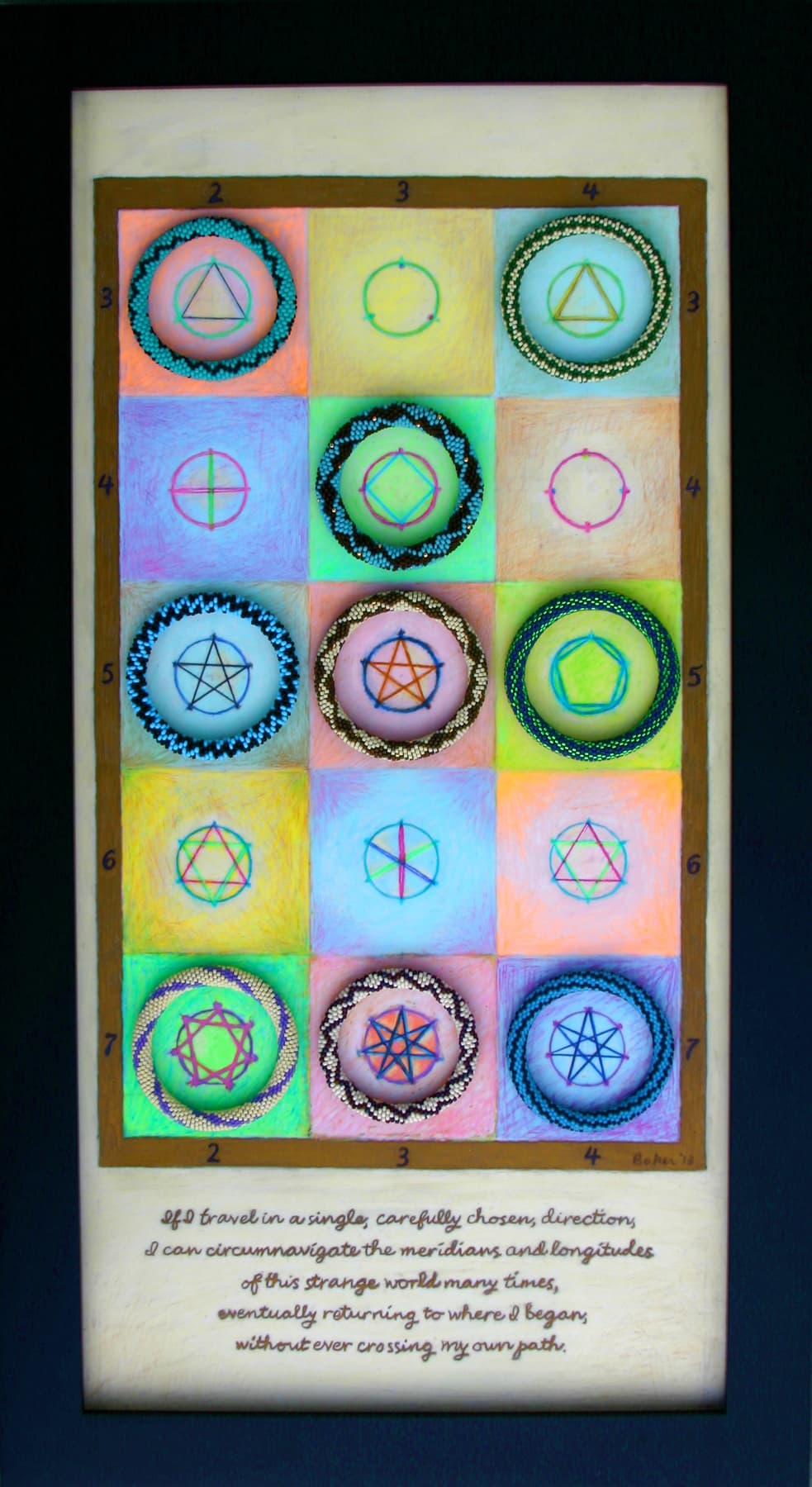
The Torus Traveler's Journey
10 x 20 inches
Bead crochet (glass beads and thread), colored pencil on mylar.
2013