Mike Naylor
Artists
Mike Naylor
Artist, COO DragonFjord Puzzles
DragonFjord Puzzles & Games
Vanvikan, Norway
Statement
I enjoy representing mathematical patterns and structures in creative ways that invite reflection and exploration.
Artworks

2-3-4-5 (set with Pisces II, Three Kings, Before Twilight and 125)
80 x 60 cm
Digital printing on canvas frames
2014-2015
This set of 4 pictures is designs based on the digits in counting sequences in bases 2, 3, 4 and 5. "Pisces II" is a double pair of fish created with binary numbers from 0000 to 1111. "Three Kings" is a set of three faces made with two sets of trinary numbers 000 to 222, the sequences are reflections of each other. "Before Twilight" shows a lonely figure climbing steps which are created with quaternary numbers 0000 to 3333. "125" is a five-pointed star made from the first 125 integers in base five: 000 to 444.
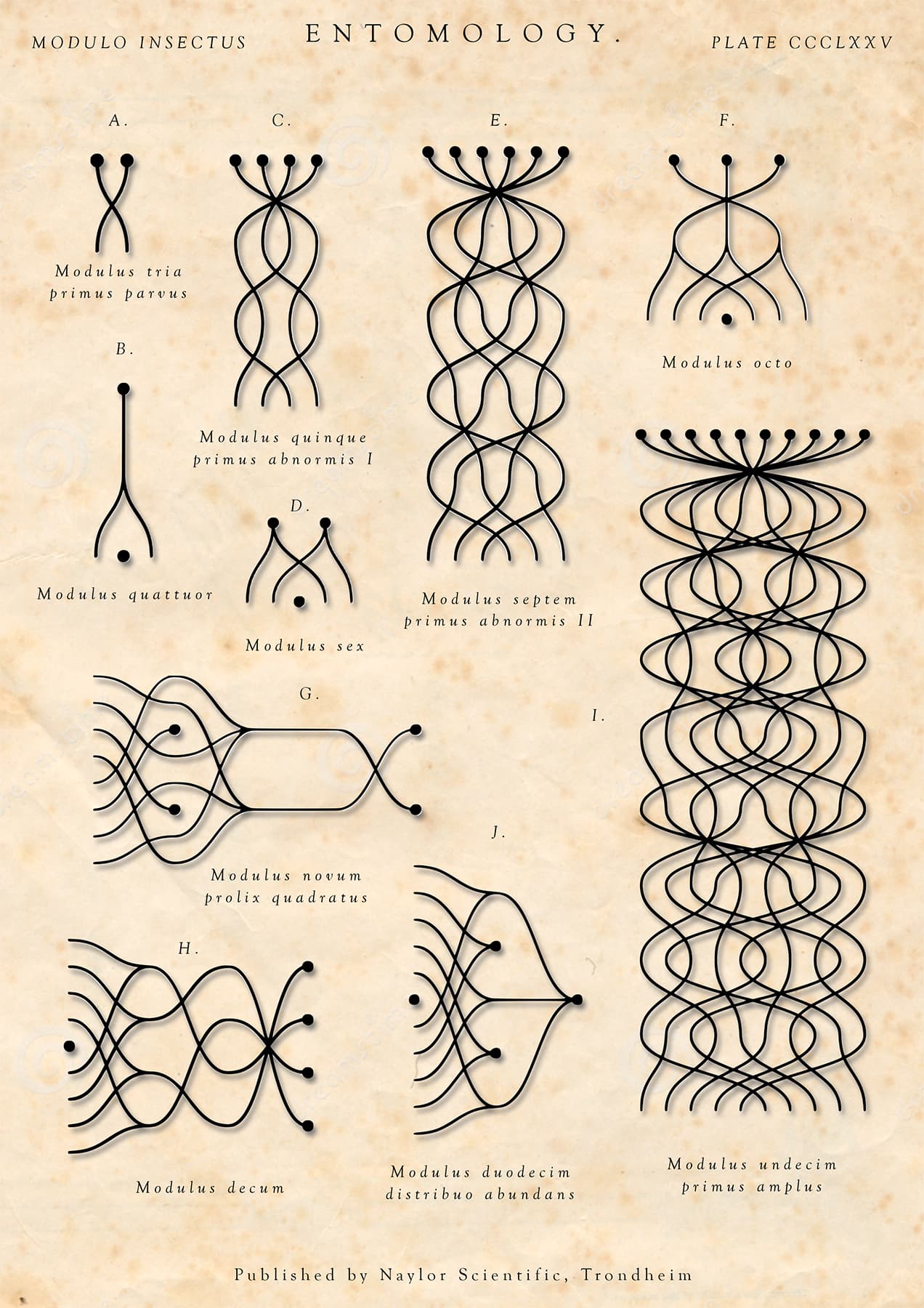
Entomology: Modulo Insectus
30 x 20 cm
Framed parchment
2014
This work shows an entomological collection of math bugs, representing factorial multiplication in modulo systems from mod 2 to mod 12. The "tail" of each bug contains strands that represent numbers 1 through n–1. These strands then move a position corresponding to the result of that number times 2, modulus n. These results are then multiplied by 3, then 4 and so on. If the result of a multiplication is 0 mod n, the strand is terminated with a dot. Prime number bugs are of maximum length, and properties of multiplication in these mod systems can be observed. Details of the construction of these bugs can be found in the 2015 Bridges proceedings.