Douglas G Burkholder
Artists
Statement
Long-long ago in a place far-far away, my love of art was placed on the back burner as science and mathematics consumed my life. My love of geometry and my desire for visualization for the sake of mathematical understanding has always been central to my teaching and comprehension. Only decades later have I begun to explore the artist within and attempted to merge art with my mathematics. Currently, my math and art seeks beauty and patterns within Conway and Radin’s non-periodic Pinwheel Tiling of the plane.
Artworks
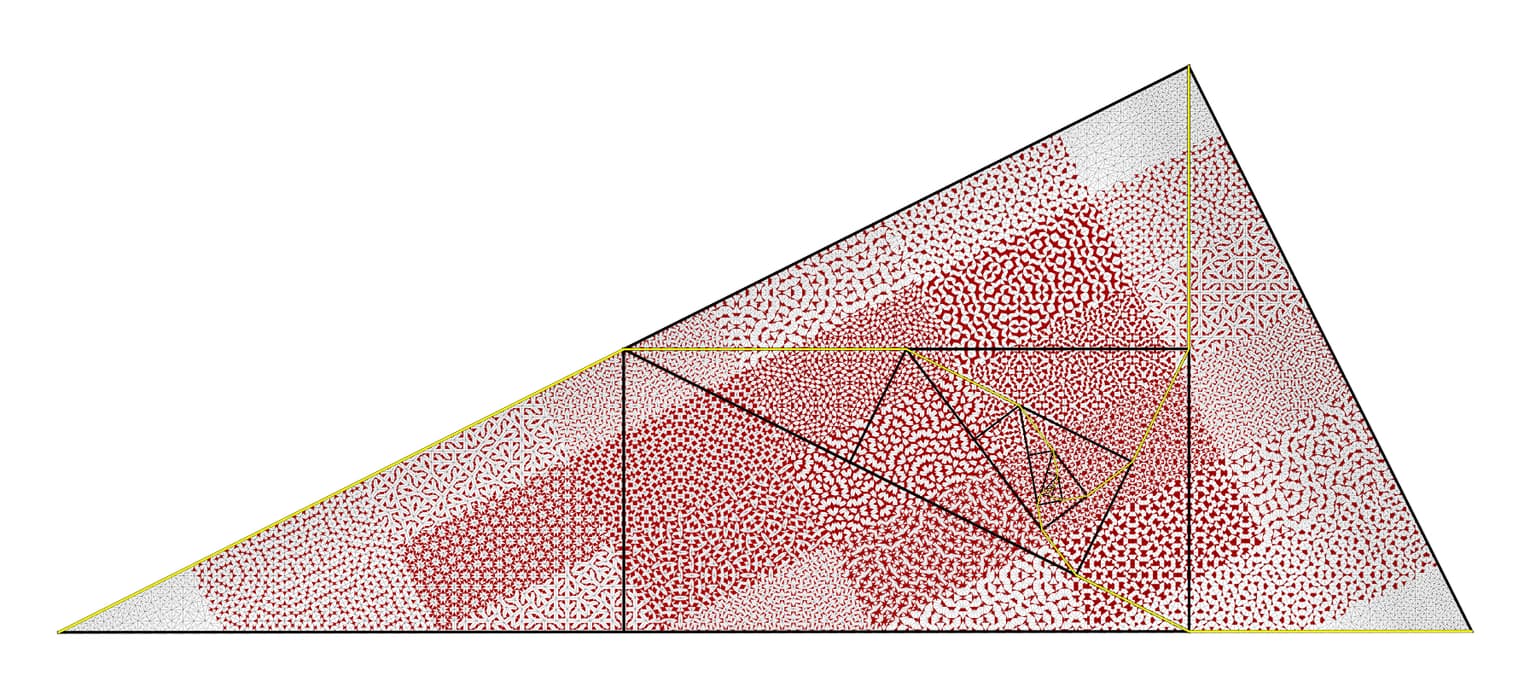
A Quilted Triangle
40 x 90 cm
Digital Print
2015
A Quilted Triangle starts with seven iterations of Conway and Radin’s non-periodic Pinwheel Tiling procedure. At the final iteration, we label each triangle one of five types based upon its location in the previous triangle. Next, we paint the interior of about 30% of the 15,625 triangles by dividing the large triangle into five rows and five columns. We paint the interior of all of the triangles of type 1 located in either the first row or the first column, etc. Thus, we paint the interior of exactly two out of every five triangles in each of the rectangular intersections of distinct rows and columns. The artwork also contains representatives of the iterative process of the Pinwheel Tiling spiraling into the triangle.
A Radin-Conway Quilt
60 x 60 cm
Digital Print
2015
A Radin-Conway Quilt starts by cutting a square with fringe containing almost a million 1x2 triangles from Conway and Radin’s non-periodic Pinwheel Tiling. Next, we paint about 30% of the triangles by dividing the square into five rows and five columns. The interior of a triangle is painted depending only upon its relative location in the next larger triangle of the tiling procedure and upon its row and column. Thus all triangles located in position 1 of their larger triangle are painted in the first row and in the first column, etc. Exactly two out of every five triangles are painted in each of the rectangles of intersections of distinct rows and columns. This quilt contains all non-trivial combinations of painting the five types of tiles.