2015 Joint Mathematics Meetings
John Shier
Artists
Statement
It has recently been found that a boundary of any shape can be completely filled with ever-smaller shapes in the limit of an infinite number of shapes. In two dimensions the areas of the shapes must obey a negative-exponent power law versus shape number i, with an exponent c such that 1
Artworks
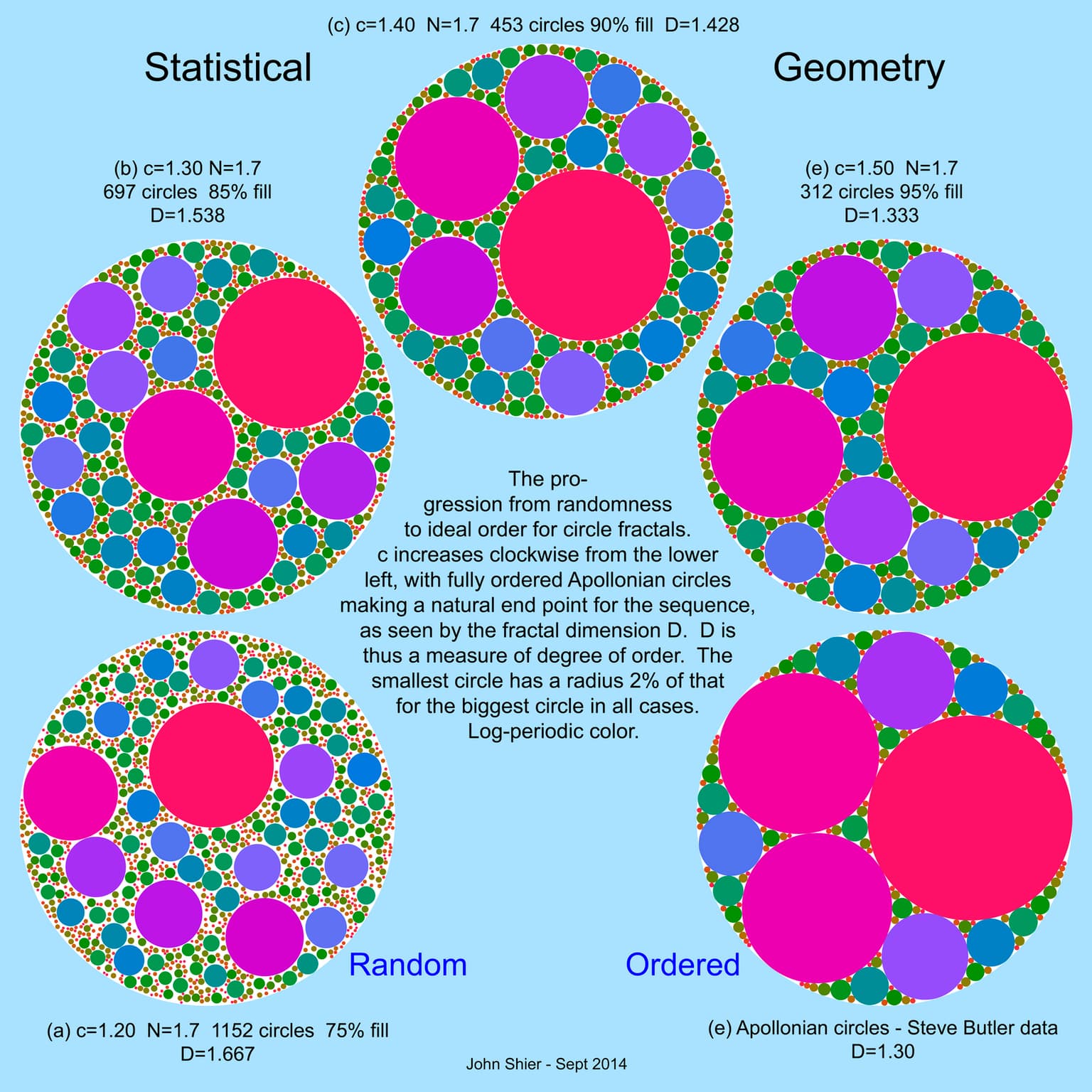
Structures involving randomness are unusual in mathematics, so it is of interest to make a connection with what is known. The statistical geometry algorithm works with power-law exponents c over a wide range (but c > 1). For triangles a central feature of increasing c is increasing order. The well-known Apollonian circles construction provides a natural end point for this sequence, with a fractal dimension D which fits nicely with D for the statistical geometry structures.