Paige MacDonald and Michael Klug

Statement

This work displays a combination of two different pieces of mathematics - the Platonic solids and the Hopf fibration. The Ancient Greeks recognized that there are exactly five Platonic solids - the tetrahedron, hexahedron (cube), octahedron, dodecahedron, and icosahedron. The Hopf fibration, discovered by Heinz Hopf in 1931, gives a way of decomposing the 3-sphere into disjoint circles that are parameterized by points on a 2-sphere. For each platonic solid we chose the vertices of that solid on the 2-sphere and looked at the inverse image of those vertices under the Hopf fibration. We then used stereographic projection to project onto 3-dimensional space, and then projected the resulting image onto a plane.

Artworks

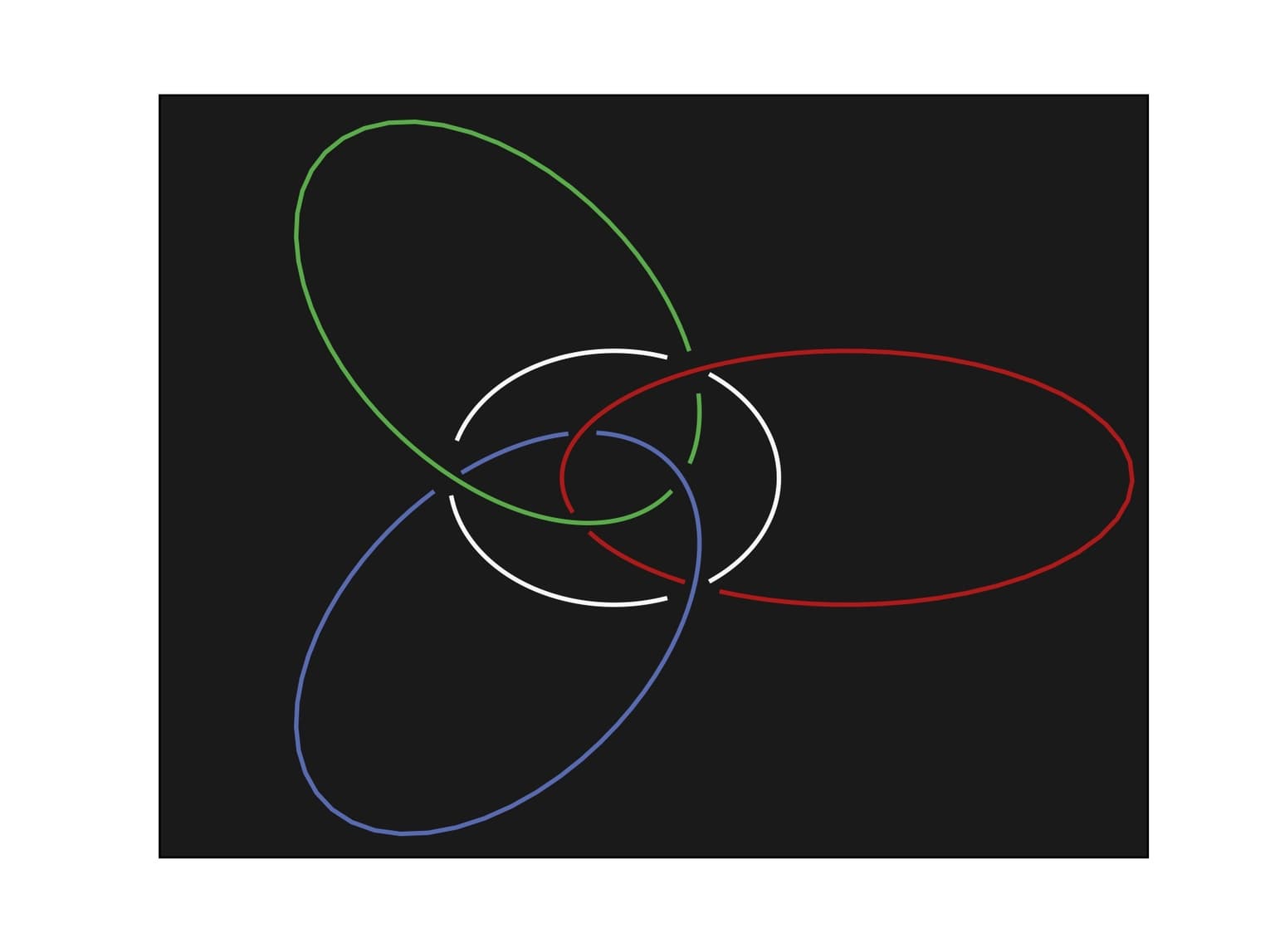
The four vertices of the tetrahedron were first inscribed in a 3-dimensional sphere, and then their fibers under the Hopf fibration were projected onto the plane. Each fiber of the Hopf map is a circle, where each circle is linked.

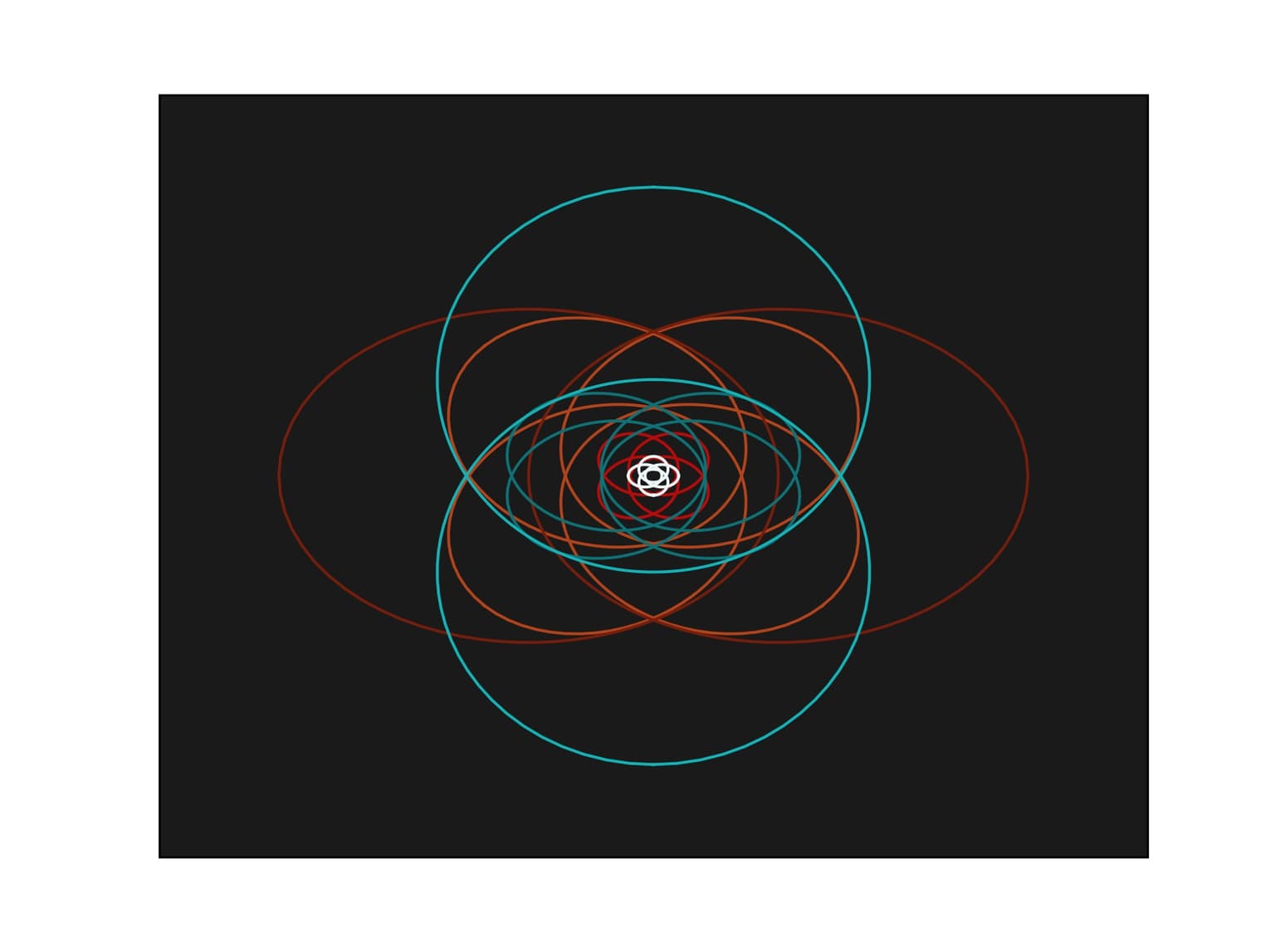
The fibers of the vertices of the dodecahedron under the Hopf fibration, projected onto the plane.