Florence Maas-Gariépy
Artists
Florence Maas-Gariépy
Studebt in mathematics
Mathematics department, Université du Québec à Montréal
Montréal. Québec, Canada
Statement
I use a colored version of the Robinson-Schensted-Knuth insertion to visualise easily the set of all pairs of tableaux generated through the insertion process or the tableaux obtained through the insertion of large permutations.
Artworks

Colored RSK Insersion of S6
60 x 60 cm
computer generated graphics printed on paper
2018
A colored version of the Robinson-Schensted-Knuth insertion applied to all permutations in the symmetric group S6. The RSK insertion provides the proof that the number of pairs of standard n-Young tableaux of same shape is equal to the number of permutations in the symmetric group Sn. The colored version of the algorithm allows to visualise easily the set of all pairs of tableaux generated through the insertion process.
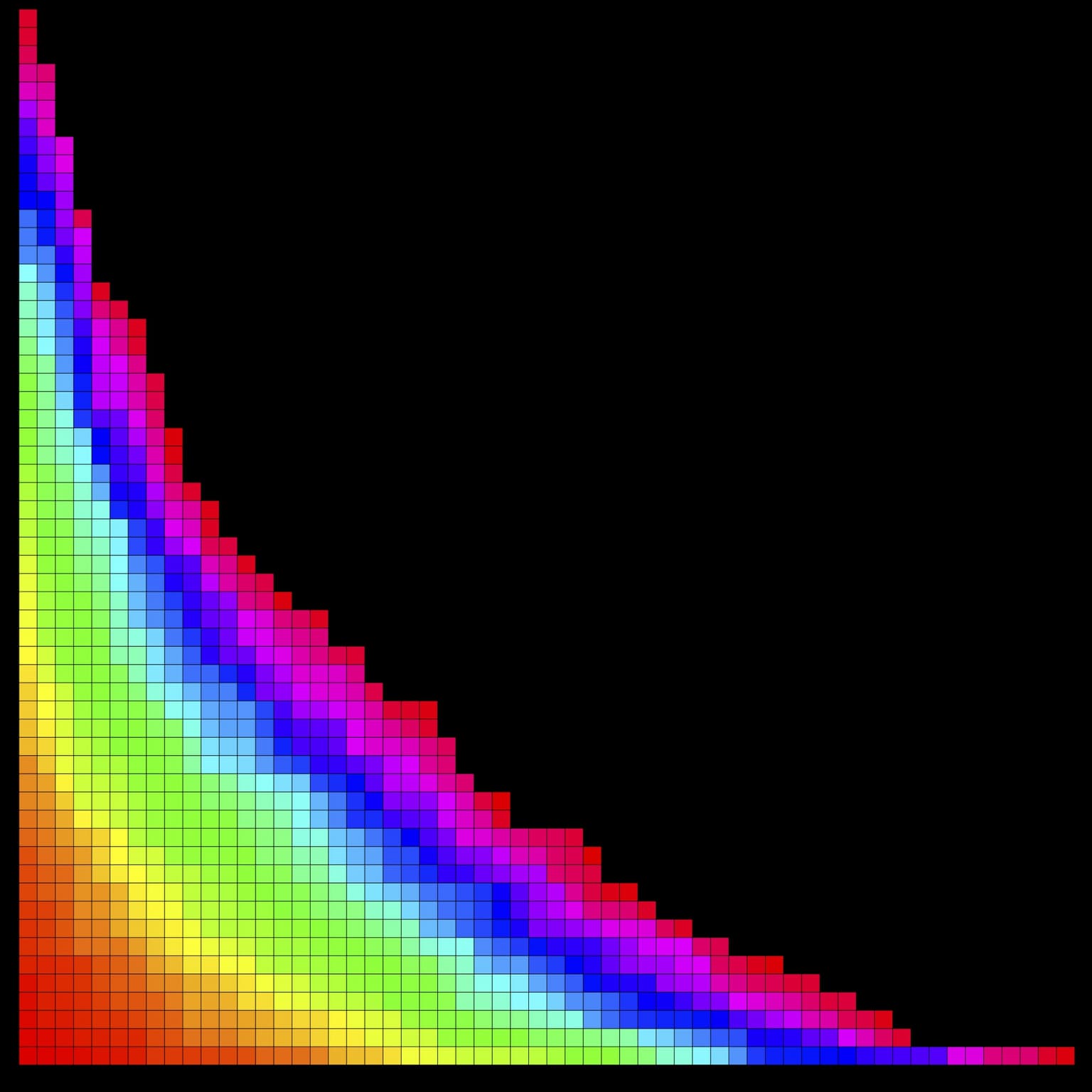
RSK Insertion of a Random Permutation of 1000
30 x 30 cm
computer generated graphics printed on paper
2018
A colored version of the Robinson-Schensted-Knuth insertion applied to a random permutation of the symmetric group S1000. The colored version of the algorithm allows to visualise the behavior of the insertion of large permutation, especially concerning the distribution of the fillings and the shape of the outer bend.