James Mai
Artists
James Mai
Professor of Art
School of Art, Illinois State University
Normal, Illinois, USA
Statement
My recent work has focused on the combinatoric development of shape-partitions, graphic adaptations of integer partitions. The set of shape-partitions of a rhombus containing nine points comprises 30 partition groups, totaling 593 distinct forms after the elimination of symmetric redundancies. This large set is divided into subsets for use in compositions. The structural features of the forms and their coherence as a set are themselves put forward as aesthetic content in my artworks—they are intended to be seen and known. To that end, I make decisions regarding color, scale, position, and orientation to reveal the multiple levels of order in each given form-set.
Artworks
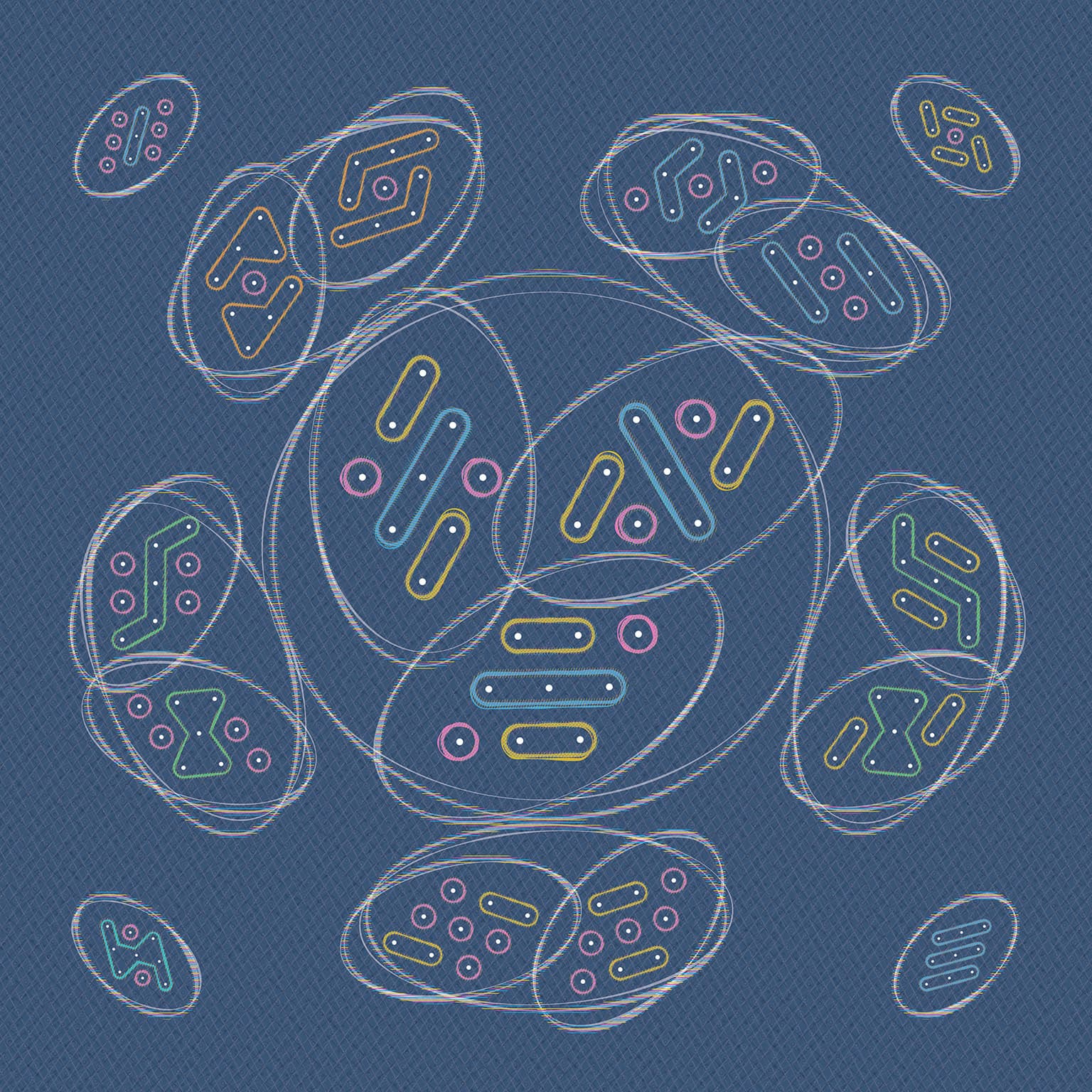
Whorls
20 x 20 cm
archival inkjet print
2019
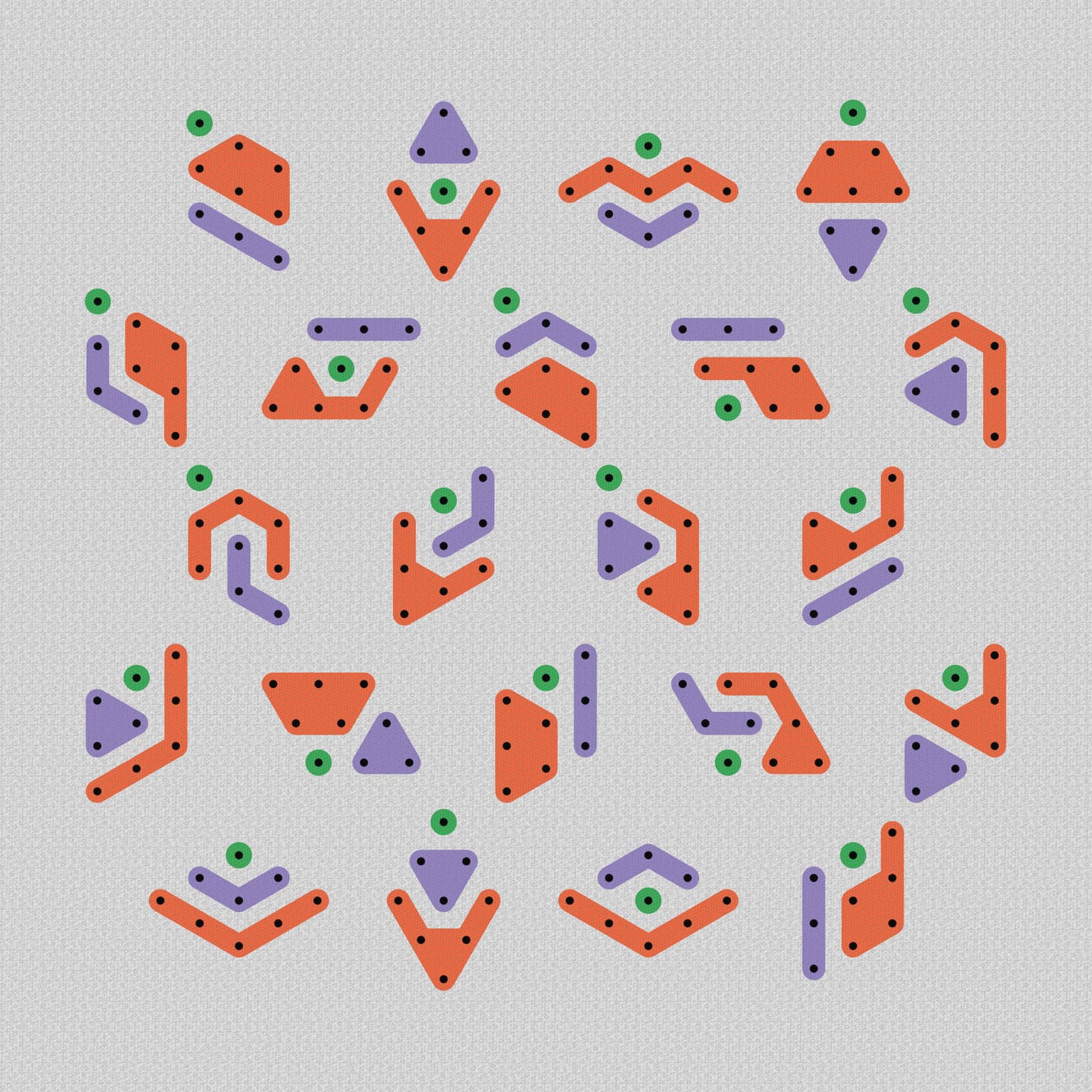
Scatter
20 x 20 cm
archival inkjet print
2019