Christopher Hanusa
Artists
Christopher Hanusa
Professor of Mathematics
Queens College, City University of New York
Queens, New York, USA
Statement
I use computational software to design images and sculpture inspired by the inherent beauty of mathematics. I am inspired by mathematical concepts, research topics, and found math. When I create art I work to understand the underlying theory, implementing it through algorithms, and honing the aesthetics to appeal to and reach a greater population. I ask: How can I develop an algorithm to expand the seed of an idea into a general phenomenon? How can I take a concept from the two-dimensional world and represent it faithfully in three dimensions? What is the artistic relationship between randomness and deliberation?
Artworks
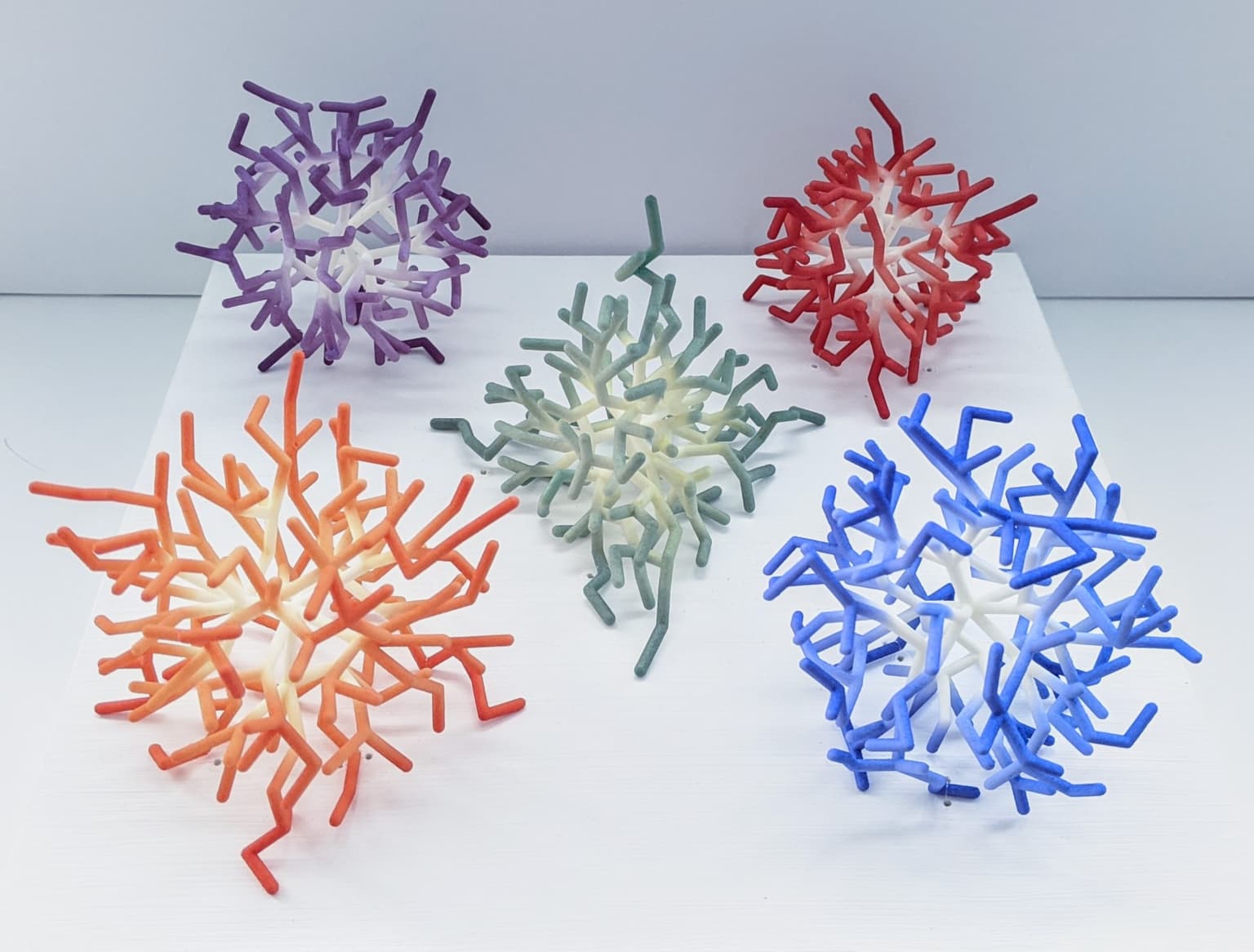
Platonic Neurons consists of five sculptures that straddle the domains of mathematics, computer science, and biology. These polyhedral neurons are created by choosing random points inside the solid, procedurally weighting the distances between them, and using Kruskal's algorithm to find a minimum weight spanning tree that connects all the points. Just as in a neuron, the center of each sculpture serves as the hub of the network. There is one sculpture for each of the classic platonic solids (Tetrahedron, Cube, Octahedron, Dodecahedron, and Icosahedron). The neurons are individually 3D printed in nylon and carefully hand dyed to create a vibrant radial gradient.