Aiman Soliman
Artists
Aiman Soliman
Research Scientist
NCSA - University of Illinois Urbana-Champaign
Champaign, Illinois, USA
Statement
Mathematical art is a unique form of artistic expression. Unlike other forms of art, the rigor of mathematics provides a guide for the imagination, although it could be restrictive sometimes compared to free artistic expression. Yet, these strict mathematical rules allow for judging, objectively, the success of an art project. I also find that mathematical artists share a similar experience with scientists in that solving a problem will usually lead to discovering another and, therefore, the continuation of their work in a natural way.
Artworks
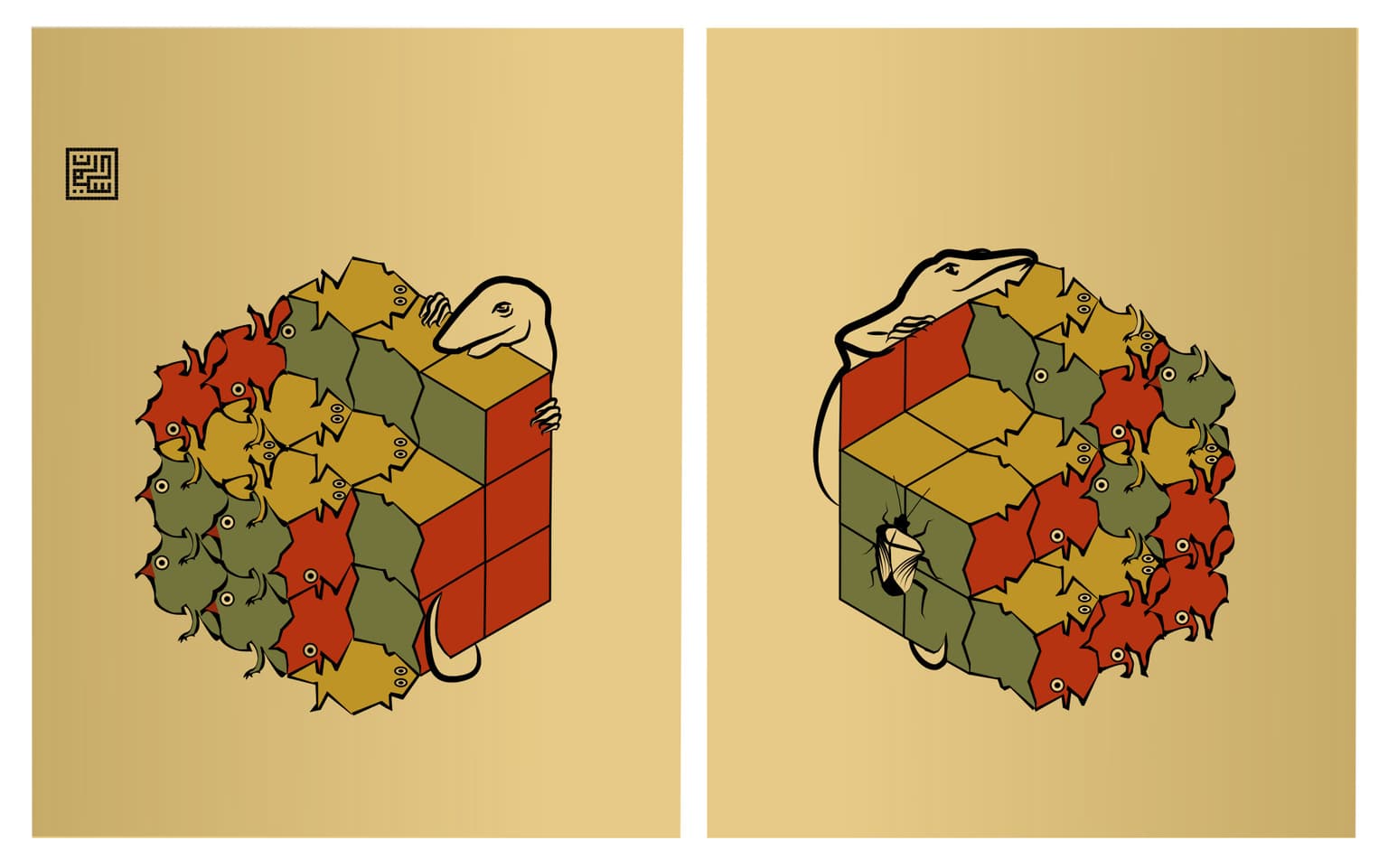
The Calissons Diptych
32 x 50 cm
Archival Digital Print
2021
This work presents an artistic depiction of the classic Calisson geometry. The Calisson problem is about filling a hexagon space using rhombuses in the three different orientations, which are permissible by the rhombus shape. Regardless of the configuration used to pack the hexagon space with rhombuses, we will always end with an equal number of rhombuses from the three orientations. Here, I present the three orientations as a fish, a lizard, and a bird with matching edges to fill the space with no gaps. A parquet deformation transforms the motifs to 3D cubes following the intuitive proof without words of this problem suggested by David and Tomei in 1989, which is ‘unfortunately’ subject to optical illusions.