Margaret Kepner
Artists
Margaret Kepner
Independent Artist
Washington, District of Columbia, USA
Statement
I enjoy expressing mathematical concepts through attributes such as color, geometric forms, and patterns. I have a background in mathematics, which provides me with a never-ending supply of subject matter, while my lifelong interest in art gives me a vocabulary and references to use in my work. Recently, I have been experimenting with grids, tilings and geometric packing problems, as well as the patterns that can be found in integer sequences such as primes, triangular numbers, and Fibonacci numbers when displayed in various formats.
Artworks
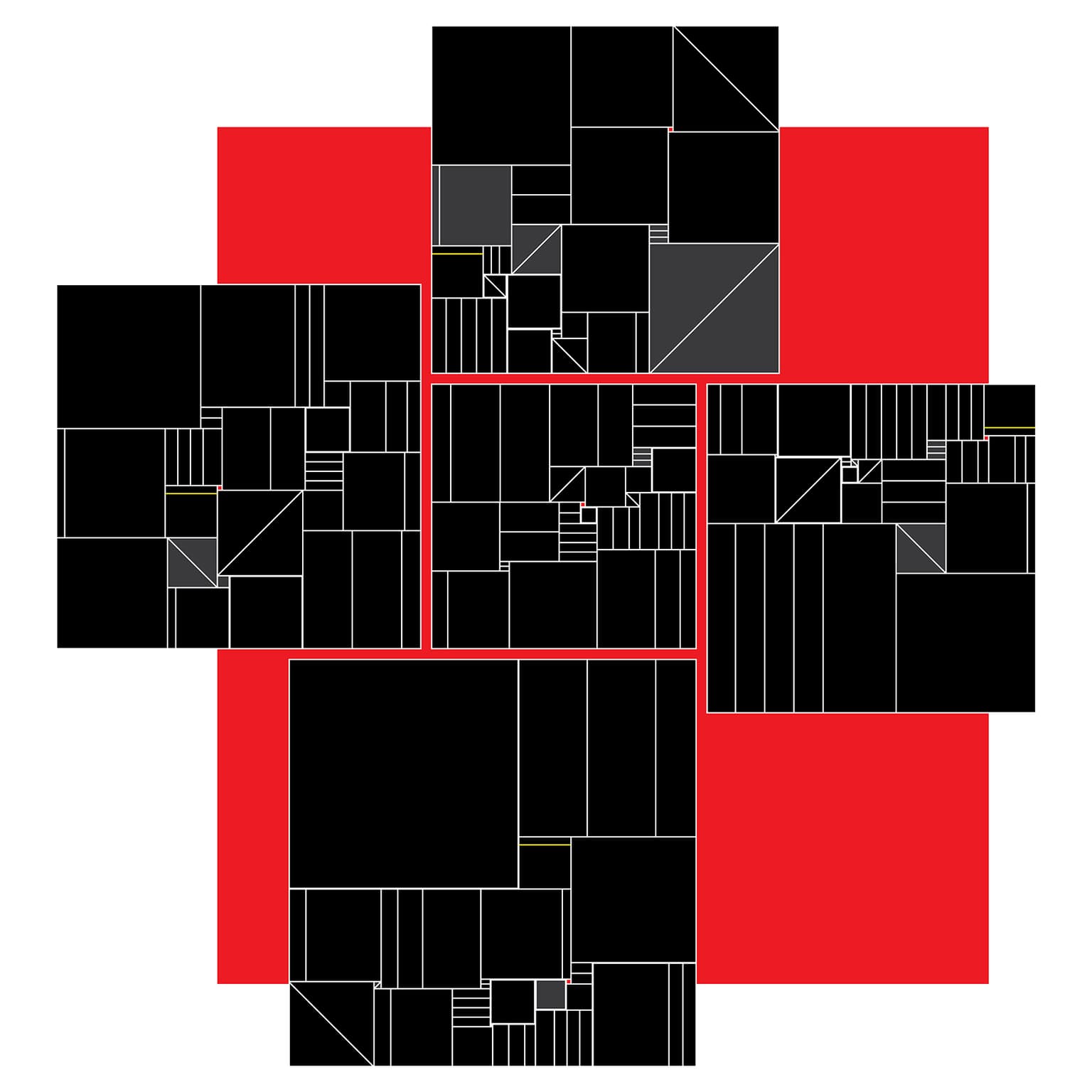
A Quintet of Squared Squares
50 x 50 cm
Archival Inkjet Print
2021
This composition is based on five Simple Perfect Squared Squares (SPSSs). Each square is a solution to the problem of packing squares within a larger square such that: there is no residual space, all the interior squares have integer sides with no repeats (perfect), and there are no smaller rectangles contained within the packing (simple). The central SPSS has 21 inner squares, which is a unique solution for that order. Four SPSSs of order 22 are arranged around the central one. The inner squares in each SPSS remain intact if their side-size is a prime, while non-prime squares are deconstructed according to a set of rules. Every SPSS contains a red 2-square, which can serve as a key to determining the dimensions in the underlying packing.