2021 Joint Mathematics Meetings
Irene Rousseau
Artists
Irene Rousseau
Artist, MFA, Ph.D
artworks in art museum internationally, exhibitions and collections
41 Sunset Drive, Summit, NJ 07901, USA
Statement
From early childhood on, I had a love for nature. In later years I began to draw natural forms that I observed. This developed into a passion to understand the structures and patterns found in these forms that I had recorded in my drawings. As an artist I aim to bridge my understanding of the underlying mathematical concepts and to metaphorically represent them as an aesthetically creative work of art.
Artworks

Stretching the Space
100 x 100 x 4 cm
oil paint on canvas
2020
My geometric painting bears a relation to structures and patterns found in natural forms. Forms in nature have a beauty of a mathematical formal order. This silent vocabulary reveals the seen and hidden structures and patterns found in the world.
My painting begins with a geometric conception on a two dimensional plane. The module serves as a unifying element and consists of a sum of multiples of these units that become an interlocking pattern and are distributed over a field. The central core consists of rotated interlocking patterns, cutting across and overlapping contour lines that result in subdivided spaces, disguising the geometry.There are linear short, sharp turns, angles as well as tessellation, symmetry and rotation.
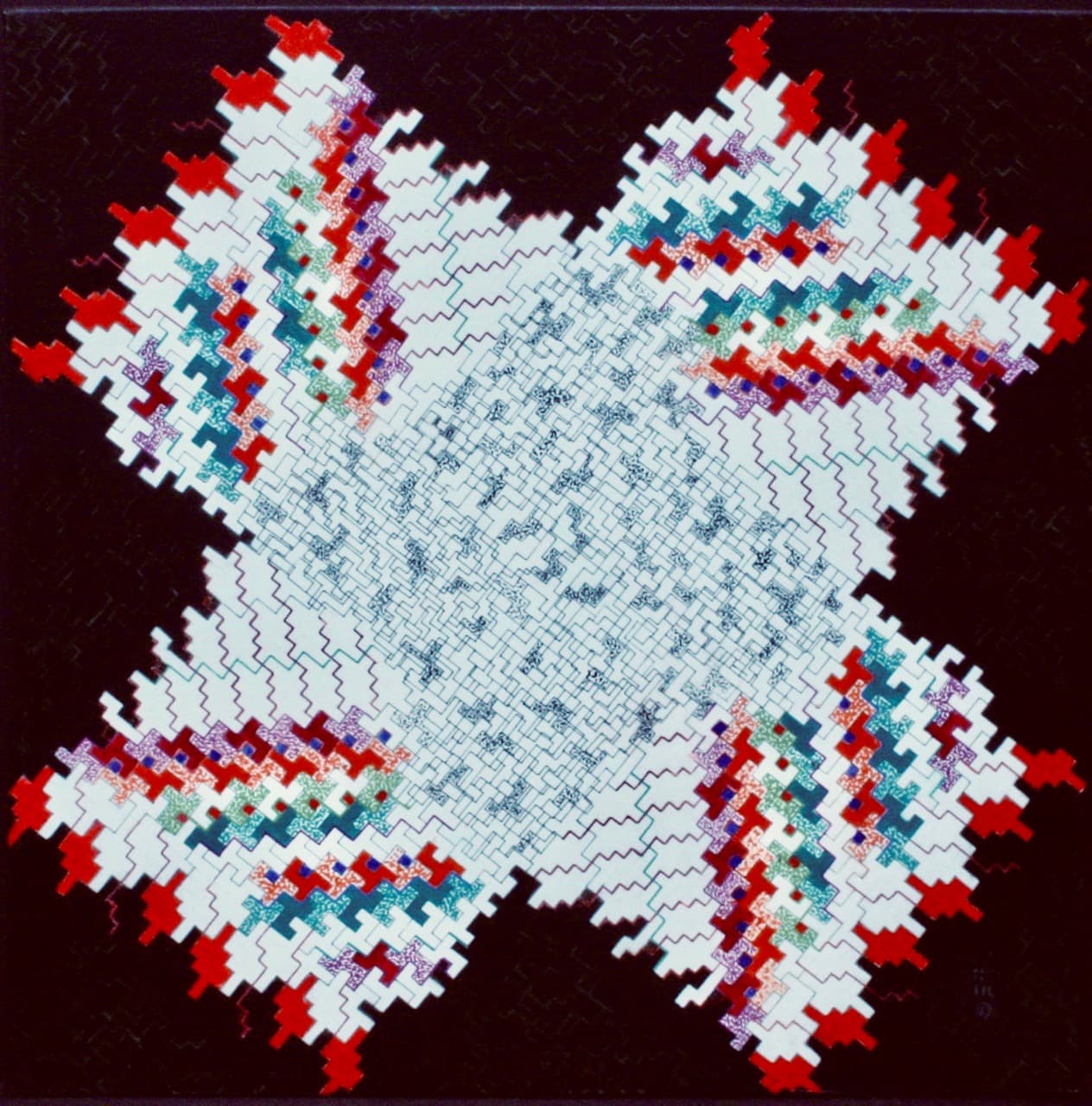
Stretching the Space
91 x 91 x 4 cm
oil paint on canvas
2020
My geometric painting bears a relation to structures and patterns found in natural forms. Forms in nature have a beauty of a mathematical formal order. This silent vocabulary reveals the seen and hidden structures and patterns found in the world.
My painting begins with a geometric conception on a two dimensional plane. The module serves as a unifying element and consists of a sum of multiples of these units that become an interlocking pattern and are distributed over a field. The central core consists of rotated interlocking patterns, cutting across and overlapping contour lines that result in subdivided spaces, disguising the geometry.There are linear short, sharp turns, angles as well as tessellation, symmetry and rotation.