Margaret Kepner
Artists
Margaret Kepner
Independent Artist
Washington, District of Columbia, USA
Statement
I enjoy expressing mathematical concepts through attributes such as color, geometric forms, and patterns. I have a background in mathematics, which provides me with a never-ending supply of subject matter, while my lifelong interest in art gives me a vocabulary and references to use in my work. Recently, I have been experimenting with grids, tilings and geometric packing problems, as well as topics in number theory such as integer sequences and partitions.
Artworks
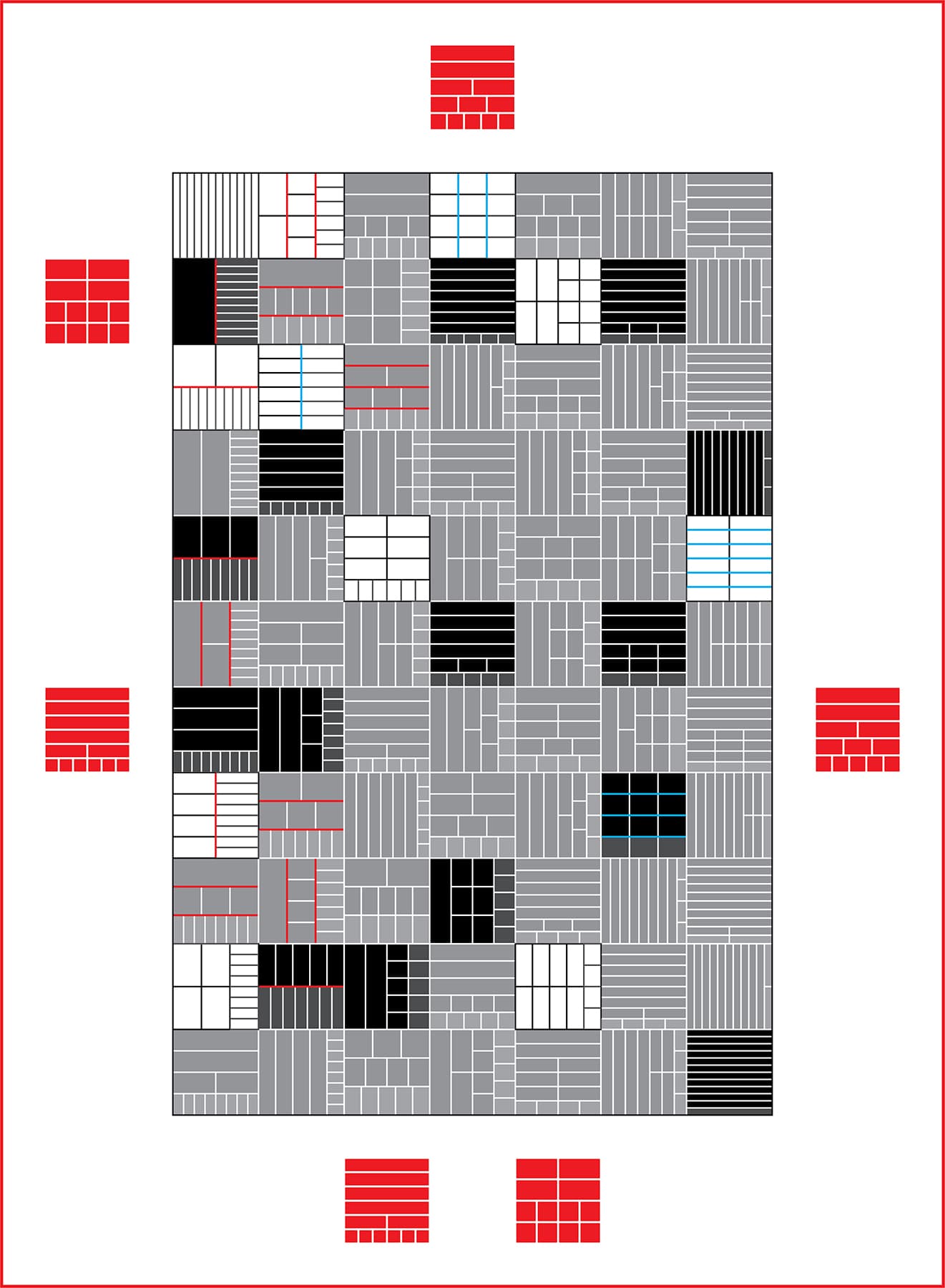
Seventy-Seven Ways to Parse a Dozen
50 x 40 cm
Archival Inkjet Print
2022
A partition of N is a set of positive integers that adds up to N. This work is an exploration of the 77 unique partitions of twelve, and their representations and properties. The square diagrams composing the piece depict partitions and resemble Young diagrams. For example, the red figure located at the top illustrates the partition 5 + 3 + 2 + 1 + 1 = 12. Various visual elements demonstrate a well-known partition theorem. Partitions with all odd terms are shown in black, and those with all distinct terms have red lines between terms. The number of partitions satisfying both conditions is equal to the number of self-conjugate partitions (in this case, three). The outer red squares serve as coordinates to locate these partitions in the grid.