2022 Joint Mathematics Meetings

Elliot Kienzle

Artists

Elliot Kienzle

Mathematics graduate student

Mathematics department, University of California, Berkeley

Berkeley, USA

ekienzle@berkeley.edu

https://chessapig.github.io/gallery/

Statement

I believe in the pedagogical power of a pretty picture. It can get people interested, keep them engaged, and sometimes make the incomprehensible click. I use art to aid and explain math, through pretty diagrams. Even when direct representation is impossible, art excels at conveying feeling. It helps communicate what mathematics makes me feel. I hope for this to make high-level math more accessible. It takes years of dedicated study to appreciate the mathematics I want to convey, but anyone with eyes can appreciate the art. I try to take the beauty we mathematicians see in symbols and put it on the page for the world to see.

Artworks

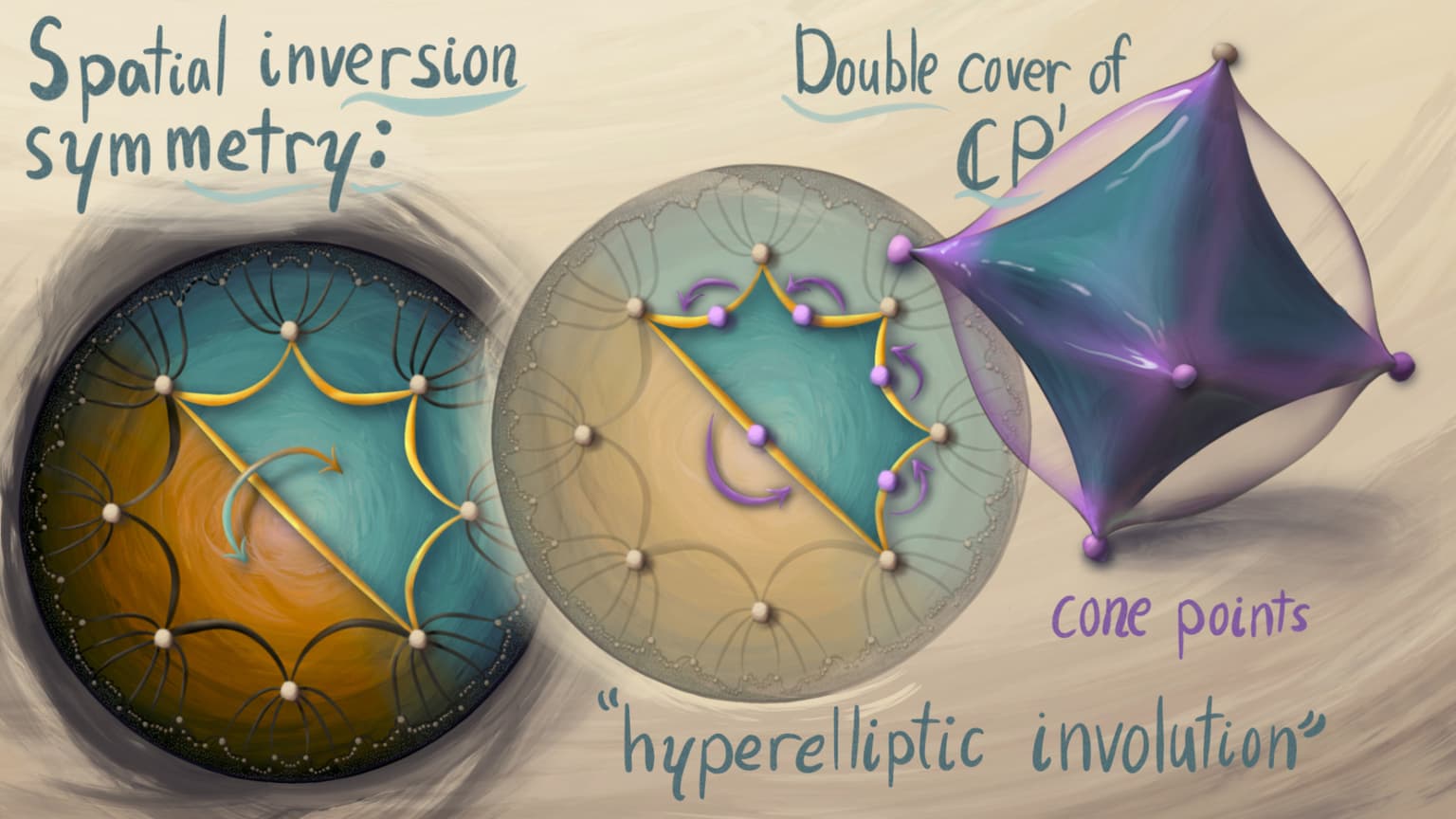
Image for entry 'Branched covers and orbifolds'

Branched covers and orbifolds

30 x 40 cm

digital

2021

A slide from a presentation of mine. This depicts a hyperelliptic curve as a branched cover of the Riemann sphere. It emphasizes the orbifold structure induced on the Riemann sphere by this covering. Each branch point looks like a cone, formed by folding an edge in half.
Image for entry 'Mathscape'

Mathscape

30 x 50 cm

Digital

2021

A panorama of a (rather biased) selection of mathematics. From left to right: ✦Chain complexes & Homology  ✦The Fano plane and octonion multiplication ✦ The E8 root lattice, which is the lattice of integer octonions ✦ Lie algebra root systems, supporting a blossoming Lie group tree  ✦ Constructing a surface by sewn discs together, using morse theory. ✦The Langlands correspondence relating Galois groups, modular forms, and adeles ✦A few surfaces, hanging out ✦A very snakey snake lemma ✦The circle doubling map applied to each pixel of an image quickly becomes static, reflecting chaos. The analogous sphere doubling map is $z \to z^2 + c$, whose dynamics describe the Mandelbrot set.