2023 Bridges Conference Art Exhibition

Margaret Kepner

Artists

Margaret Kepner

Independent Artist

Washington, District of Columbia, USA

renpek1010@gmail.com

http://mekvisysuals.net

Statement

I enjoy exploring the possibilities for conveying ideas in new ways, primarily visually. I have a background in mathematics, which provides me with a never-ending supply of subject matter. My lifelong interest in art gives me a vocabulary and references to utilize in my work. I enjoy expressing mathematical concepts through attributes such as color, geometric forms, and patterns. One topic I have explored recently is integer sequences -- their distributions, rhythms, and overlaps. When these sequences are displayed in different formats, interesting relationships are revealed. I have experimented with placing integer sequences in linear, square, triangular, and hexagonal grids.

Artworks

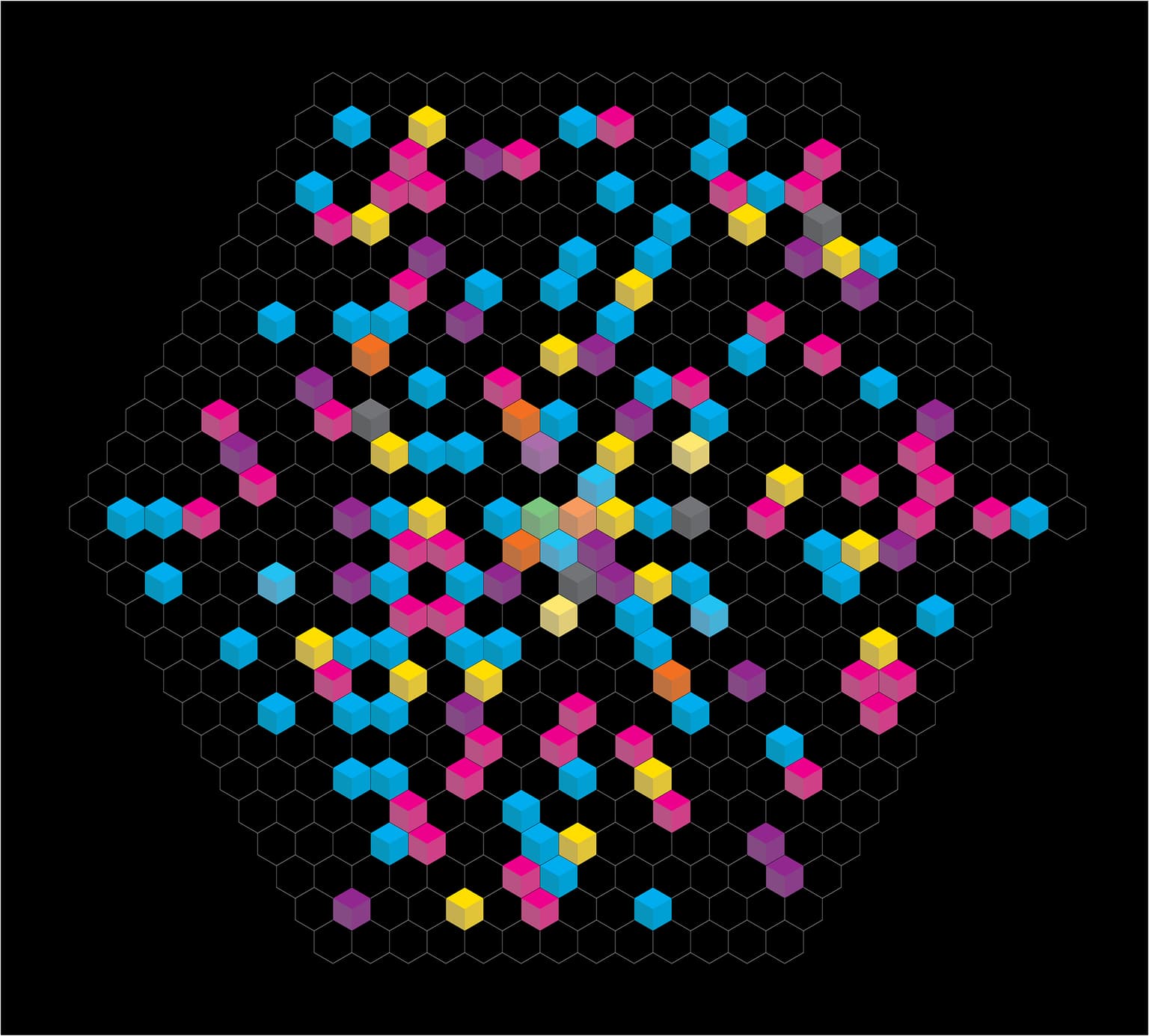
Image for entry 'Number Sequences on a Hexagonal Grid: 457'

Number Sequences on a Hexagonal Grid: 457

50.0 x 50.0 cm

Archival Inkjet Print

2023

The underlying structure for this piece is a spiral path traced out on a hexagonal grid. The path moves outward from a central hexagon (assigned the value 1) in a clockwise direction, and ends with a hexagon at the far right representing 457. Each hexagon along the path is colored according to its membership in various number sequences: primes (cyan), happy numbers (magenta), and triangular numbers (yellow). Integers occurring in more than one sequence result in mixed hues (orange, green, or purple). The Fibonacci numbers appear as transparent white hexagons layered on top. Shading produces the appearance of 3D cubes floating above the grid. Interesting patterns emerge, including several prime-heavy lines and a yellow “spiral galaxy.”