2023 Joint Mathematics Meetings
Gabriele Meyer
Artists
Gabriele Meyer
Senior Lecturer Emerita
University of Wisconsin, Madison
Madison, Wisconsin, USA
Statement
Aside from crocheting hyperbolic surfaces, I also like to make linoleum prints. My favorite subjects are sea shells. They have a variety of mathematical aspects: - snails embody spirals - the growth of clams often are dilations - the patterns on cone snails, volutes and others come about through mechanisms that are biological cellular automata. The curves of these sea creatures are just very beautiful and inspiring.
Artworks

Abalone and broken whelk
46 x 31 cm
linoleum print on paper
2022
This print shows the inside of an abalone (haliotis midae), where you can see its spiral. The other shell is a whelk, where the broken outside makes the spiral structure visible.
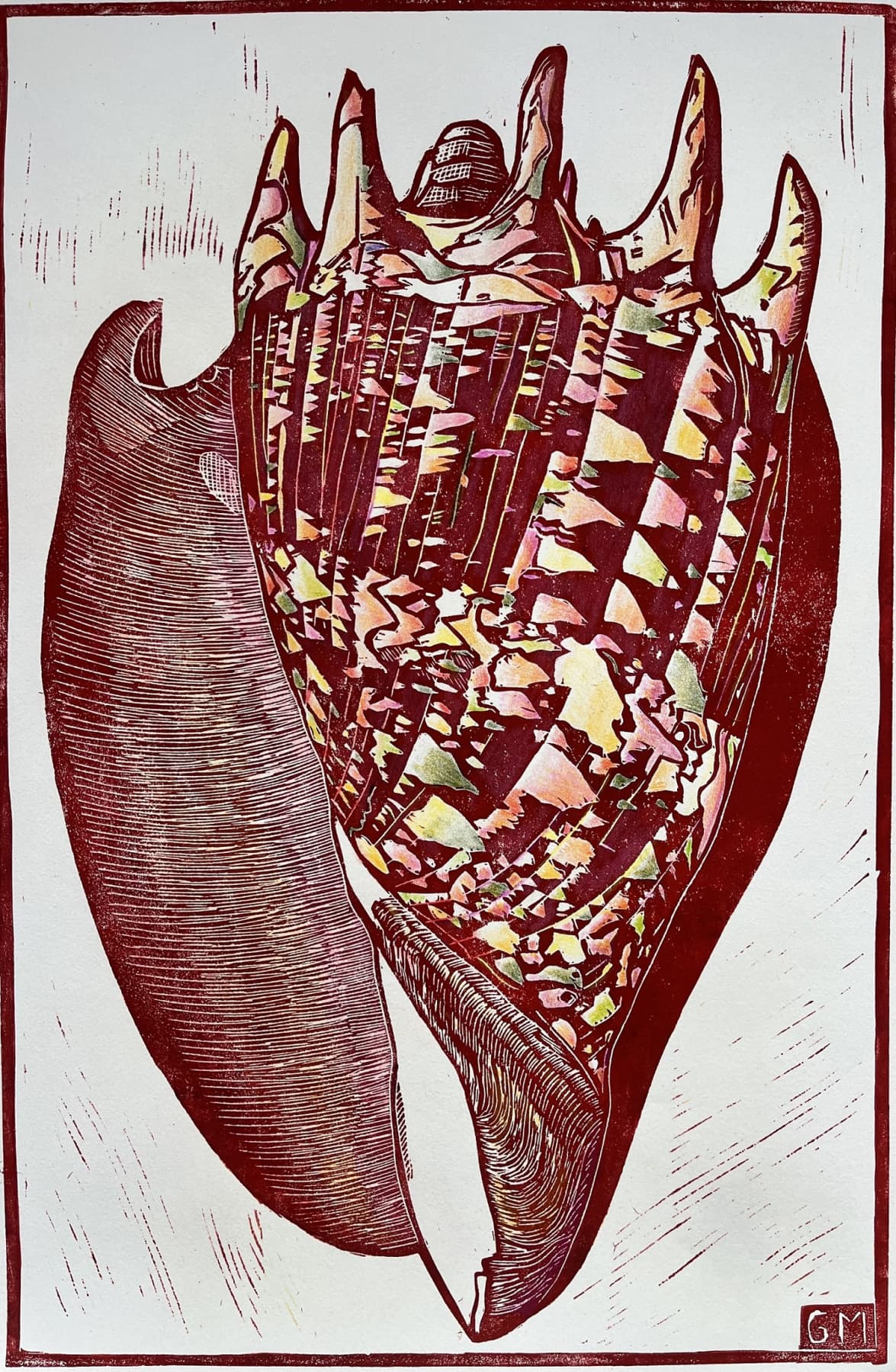
Imperial Volute
46 x 28 cm
colored linoleum print
2022
This linocut depicts an imperial volute (cymbiola imperialis). The markings on it look similar to Sierpinski triangular patterns and are generated by cellular automata, where the content of a field is determined by the contents of its neighboring fields. This process may or may not converge.
But the pattern is beautiful!