2023 Joint Mathematics Meetings
Viduranga Landers
Artists
Viduranga Landers
High School Student
D.S.Senanayake College
Colombo, Sri Lanka
Statement
Four years have passed since I made my first piece of mathematical digital art, simply a fractal. Since then, I've been obsessed with fractals and have recreated several of the most well-known fractals till the year 2021. In 2021, while attempting to generalize the Collatz conjecture, I rediscovered a part of a previously published generalization by Professor M. Bruschi. While the generalization existed as a conjecture, I was able to generate amazing fractals from it. Since then, I've utilized the generalization of the Collatz conjecture to construct a multitude of astounding fractals.
Artworks
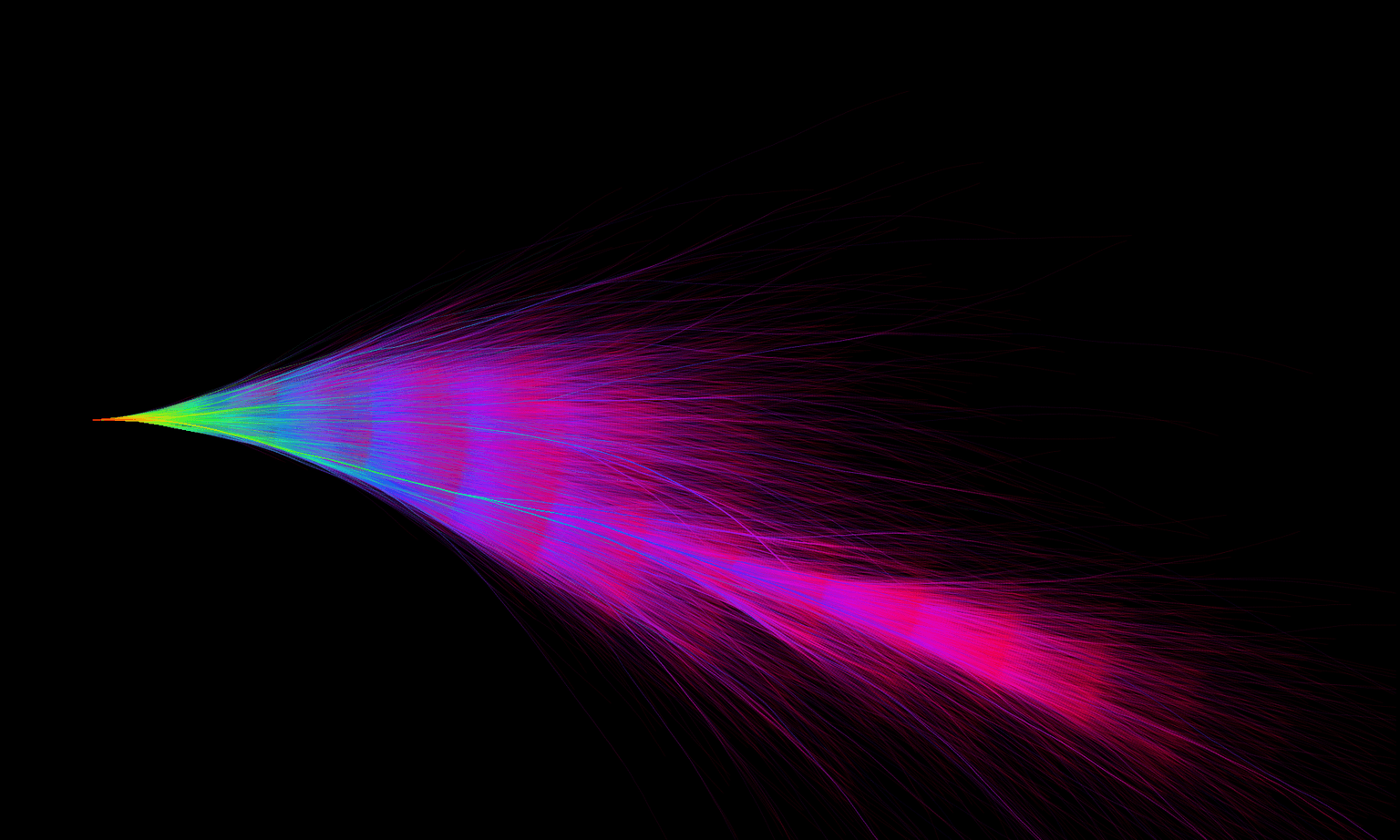
Collatz Feather 2.0
24 x 39 cm
Digital
2021
The method used to construct these fractals is nearly identical to the method used to generate the Collatz Feather fractal. As the generalized equation is applied, there are more variables that can be altered to produce unique fractals. In the generalized Collatz conjecture, the equation $3x+1$ is transformed to $(b^m + 1)n + b^m - (n$ mod $b^m)$.
The Collatz conjecture’s equation, $3x+1$, could be derived when $m = 1$. This fractal feather is also produced using an equation obtained by setting $m$ equal to $1$. Due to this and its physical appearance, I would call it Collatz Feather 2.0.

SpiraL
22 x 39 cm
Digital
2021
The method used to construct these fractals is nearly identical to the method used to generate the Collatz Feather fractal. As the generalized equation is applied, there are more variables that can be altered to produce unique fractals. In the generalized Collatz conjecture, the equation $3x+1$ is transformed to $(b^m + 1)n + b^m - (n$ mod $b^m)$.
This amazing fractal is one of a series of similar fractals formed by the equations when $m = 3$.