2024 Joint Mathematics Meetings
Gabriel Dorfsman-Hopkins, Eliza Brown
Artists
Eliza Brown
Mathematics Student
St. Lawrence University
Canton, New York, USA
Gabriel Dorfsman-Hopkins
Assistant Professor of Mathematics
Department of Mathematics, Statistics, and Computer Science, St. Lawrence University
Canton, New York, USA
Statement
The fundamental theorem of algebra states that every polynomial equation with complex coefficients has complex roots. When families of these roots are plotted on the complex plane, we obtain striking patterns called algebraic starscapes. In this series, we created starscapes from the eigenvalues of all 3x3 integer matrices within fixed bounds, sizing and coloring the roots according to the determinant. We developed python code to generate the images—utilizing techniques such as kernel cropping and gaussian blurring—and employed a supercomputer to parallelize the millions of computations. The produced images exhibit deep relationships between the geometry and arithmetic and serve as invitations to explore the mysterious patterns of integers.
Artworks

Bohemian Eigenvalue Starscape No. 7
61.0 x 61.0 cm
Digital image printed on canvas
2023
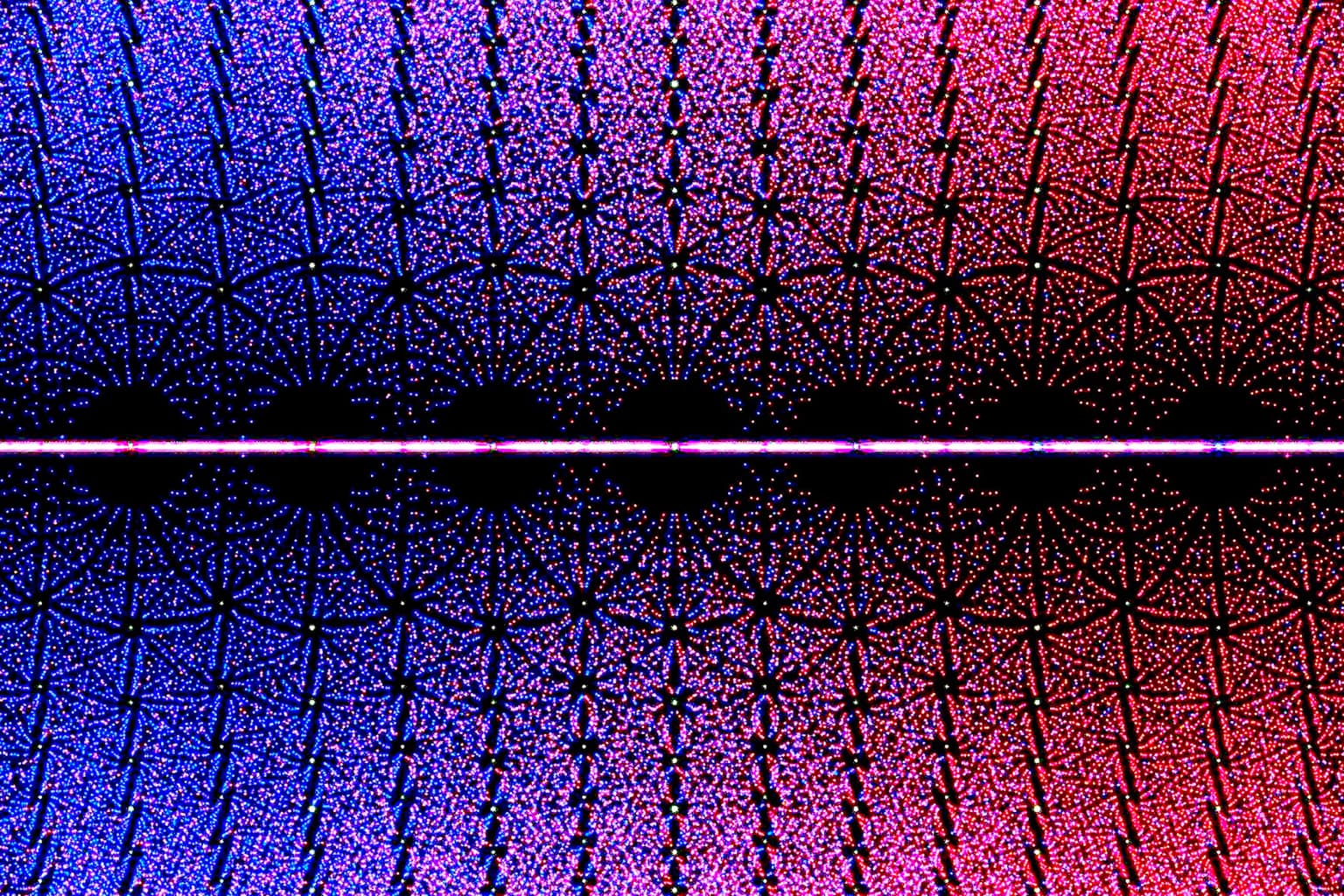
Bohemian Eigenvalue Starscape No. 4
30.0 x 45.0 cm
Digital image printed on canvas
2023