2025 Bridges Conference Math + Fashion
Violeta Vasilevska
Designers
Violeta Vasilevska
Professor
Utah Valley University
Orem, Utah, USA
Biography
I was born and raised in Republic of North Macedonia where I received my bachelor’s and master’s degree in mathematics. In 2000, I came to the US, received my doctorate degree from the University of Tennessee, Knoxville, and in 2010 joined the Department of Mathematics at Utah Valley University, where I currently hold the rank of professor. My research interests are diverse, ranging from topics in pure mathematics to topics in math education, to connections of math and art. In addition, I enjoy mentoring students through undergraduate research. I have mentored students in research projects that connect technology, math, and art (especially origami). I am passionate about teaching, and in my classes, I implement various active learning, student-centered approaches and cultivate an inclusive, interactive, and engaged environment, while showing sincere care and respect for my students and their diverse learning styles. In addition, I try to incorporate my passion for Origami, crafts, and art into my teaching through various engaging projects. Since 2007, I have been leading and participating in various outreach programs that popularize mathematics, especially ones that encourage and support women in mathematics. As a result, I have been involved and interested in researching the effects of after school math programs on the high school women’s attitude towards mathematics through my outreach program Math Girls Rock!. In addition, this outreach involvement has deepened my interest in working towards connecting math and art. I have been regularly developing projects for these outreach programs that illustrate math-art connection: various math and origami projects, projects that involve beading and knitting, projects to produce art designs using technology etc. I have received several awards recognizing my teaching excellence, service, and my outreach efforts. Among my hobbies are my love for Origami and art, reading, traveling, and learning about different cultures.
Looks

Truncated Tetrahedron Earrings and a Pendant
Photography: Mike Bird

Truncated Tetrahedron Earrings and a Pendant (with a collier necklace)
Photography: Violeta Vasilevska (edited by Mike Bird)

Truncated Tetrahedron Earrings and a Pendant (with a ribbon necklace)
Photography: Violeta Vasilevska (edited by Mike Bird)
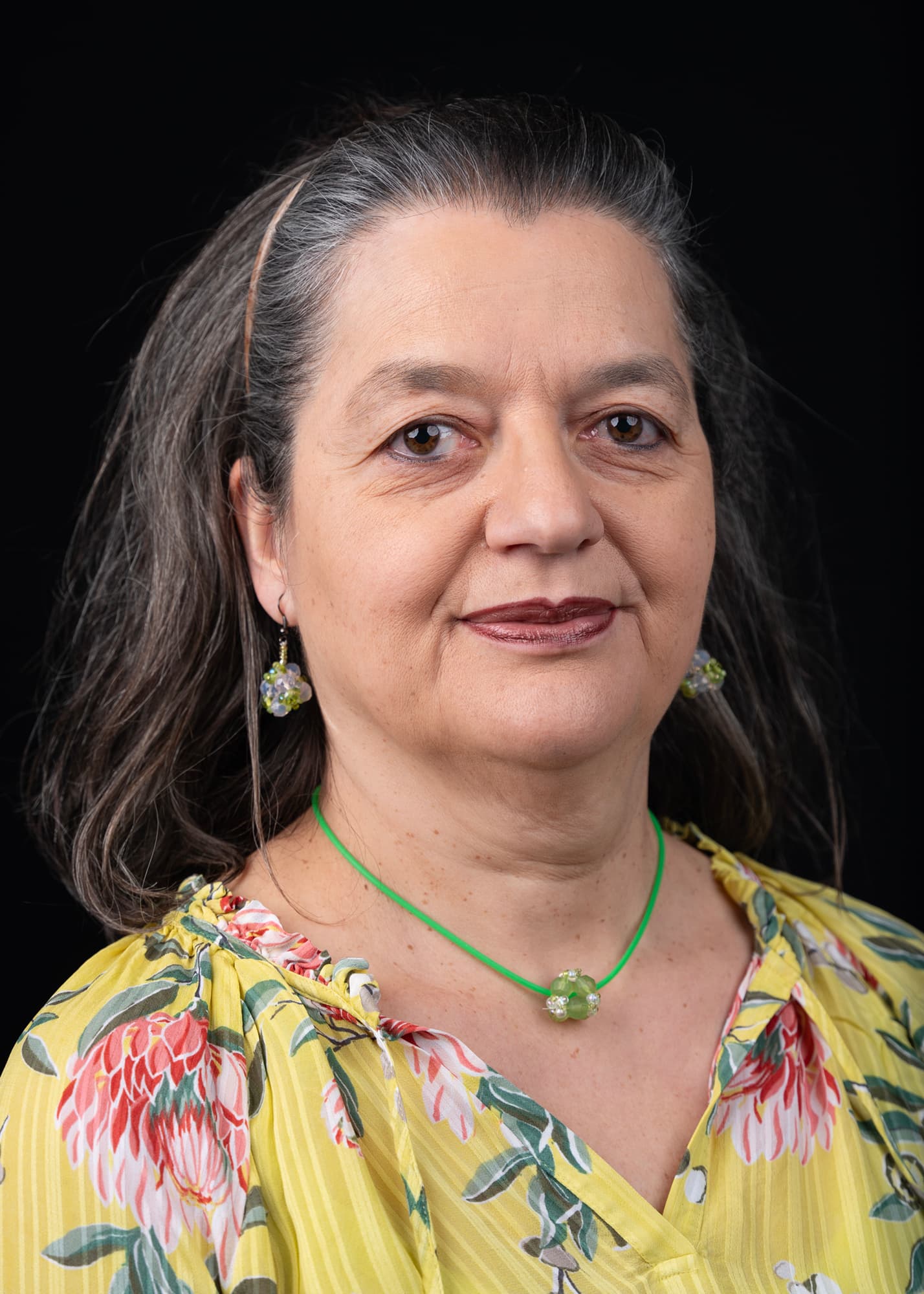
Truncated Tetrahedron Earrings and a Pendant (worn by a person)
Photography: Mike Bird Model: Violeta Vasilevska
About the look
Truncated Tetrahedron Earrings and a Pendant
Crystal beads and a beading thread
2025