Artists
Jade Mawn
Student
University of Richmond, Math and Computer Science
Richmond, Virginia, USA
Statement
As a math student, one thing that I frequently find intriguing is how we have come to visually express math concepts. For example I remember the awe of early algebra, seeing equations represent graphs and vice versa, and manipulating these elements. Or, when I first grasped derivatives through graphical visualization, rather than from rules and formulas. Throughout the past academic year I have had the pleasure of working alongside Dr. Heather Russell in her research on Webs. The visual nature of this work instantly appealed to me. My research book often reminds me of a sketchbook more so than a notebook, which is how I came to realize these webs are art as much as they are math and I do not think such a distinction needs to be made.
Artworks
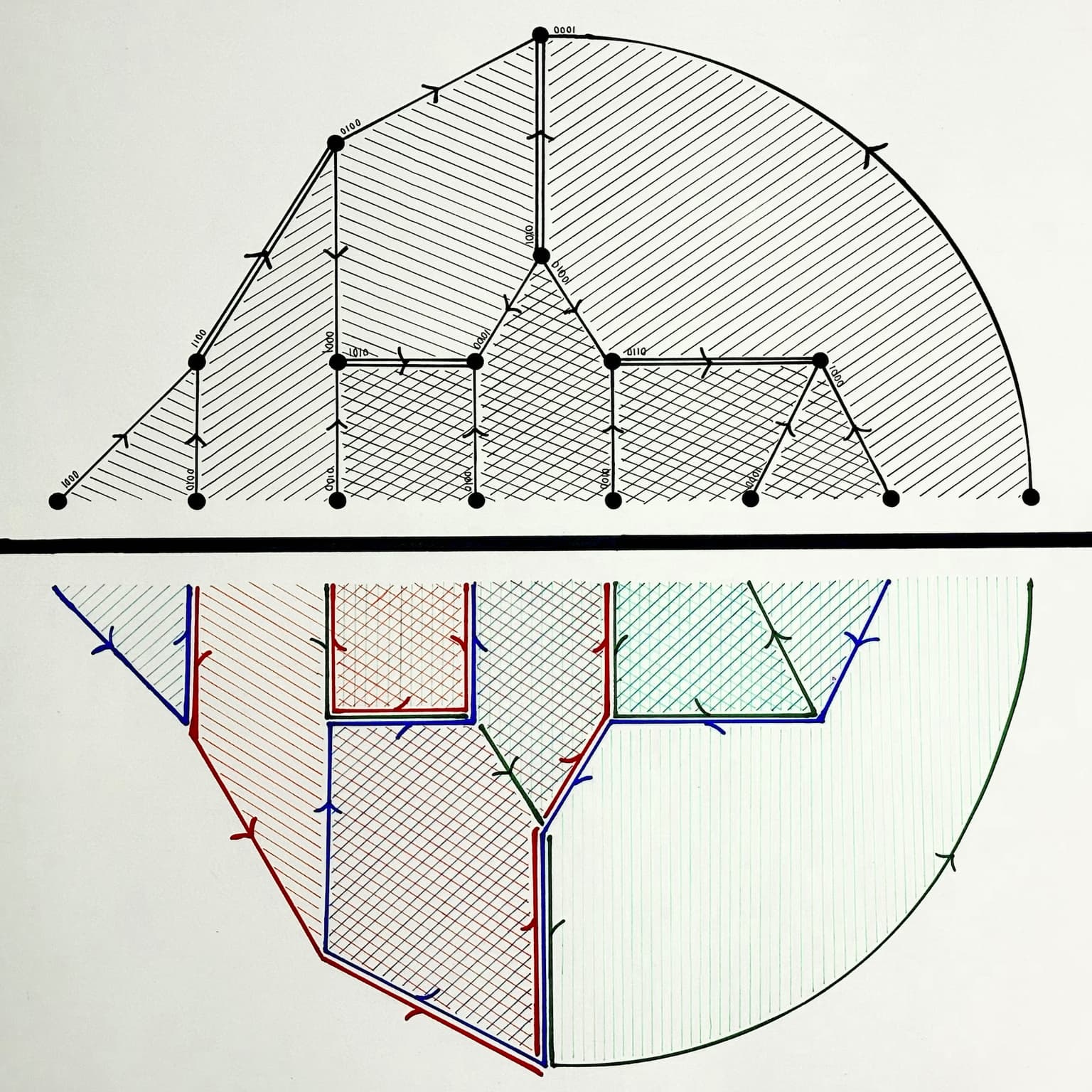
Veiling Mathematical Complexity of Webs through Color
50.8 x 50.8 cm
Marker and Pen on Paper
2024