Artists
Statement
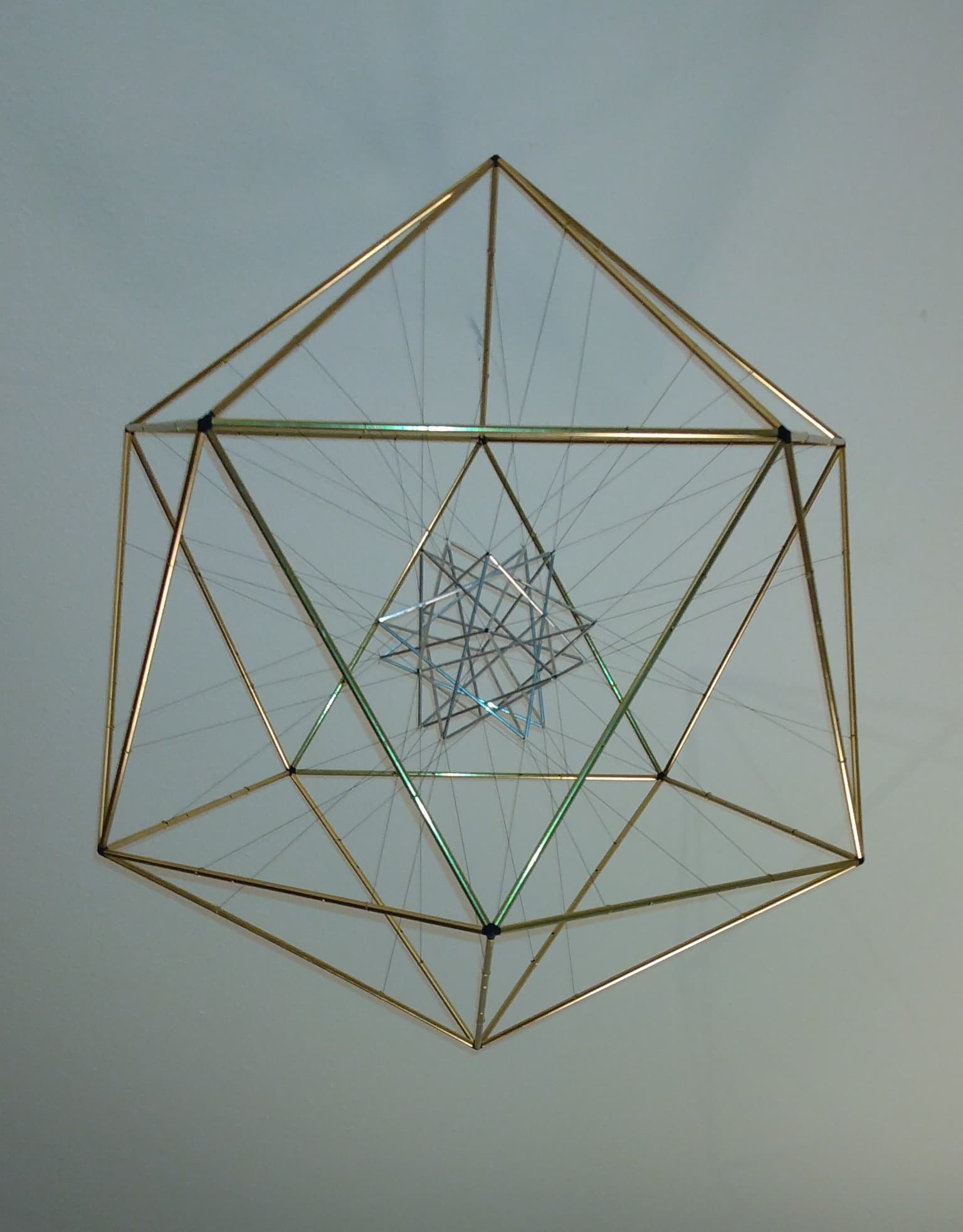
I received a Ph.D. in mathematics from Johns Hopkins. For most of my career I taught high school math in Waldorf schools, where the pedagogy encourages the bridging of mathematics and art. I'm now retired. The Platonic solids are quite simple geometric forms, and yet, as one contemplates them and builds up and holds the forms in one’s imagination, they become quite captivating. The center point has a polar plane (in the sense of projective geometry), which is the plane at infinity. One can imagine the form carved out by planes and lines coming in from the infinitely distant periphery. The model shown here is designed to suggest shapes that are not solid blocks, but rather created by lines and planes coming from the periphery.
Artworks
The compound of 5 tetrahedra, with its interplay between the symmetry of the tetrahedron and that of the icosahedron, has long fascinated me. I have now made 7 different renditions of the figure, all quite different from one another. Most have appeared in Bridges exhibitions. Last year’s piece showed the 5 tetrahedra in tensegrity with the tensegrity cables forming an icosahedron, suspended in the center. This year’s piece is that one turned inside out. The five tetrahedra are suspended inside an icosahedron. The in-radii of the icosahedron and the tetrahedron must be in the ratio of 4ϕ +3 (where ϕ =golden mean) for the extended tetrahedron edges to meet the icosahedron edges. To my knowledge this form has not appeared elsewhere.