Artists
Tis Veugen
Artist of Mathematics
Waalre, The Netherlands
Statement
My quest for Escheresque tessellations began seven years ago. Since then I have programmed and created hundreds of artworks based on hyperbolic, circular, spiral, non-periodic and fractal tessellations. Last year I designed tessellations from space-filling curves. For all these tessellations, existing Escheresque deformation schemes have been implemented in my tool Tissellator, and newly discovered schemes have been made available for public use.
Artworks
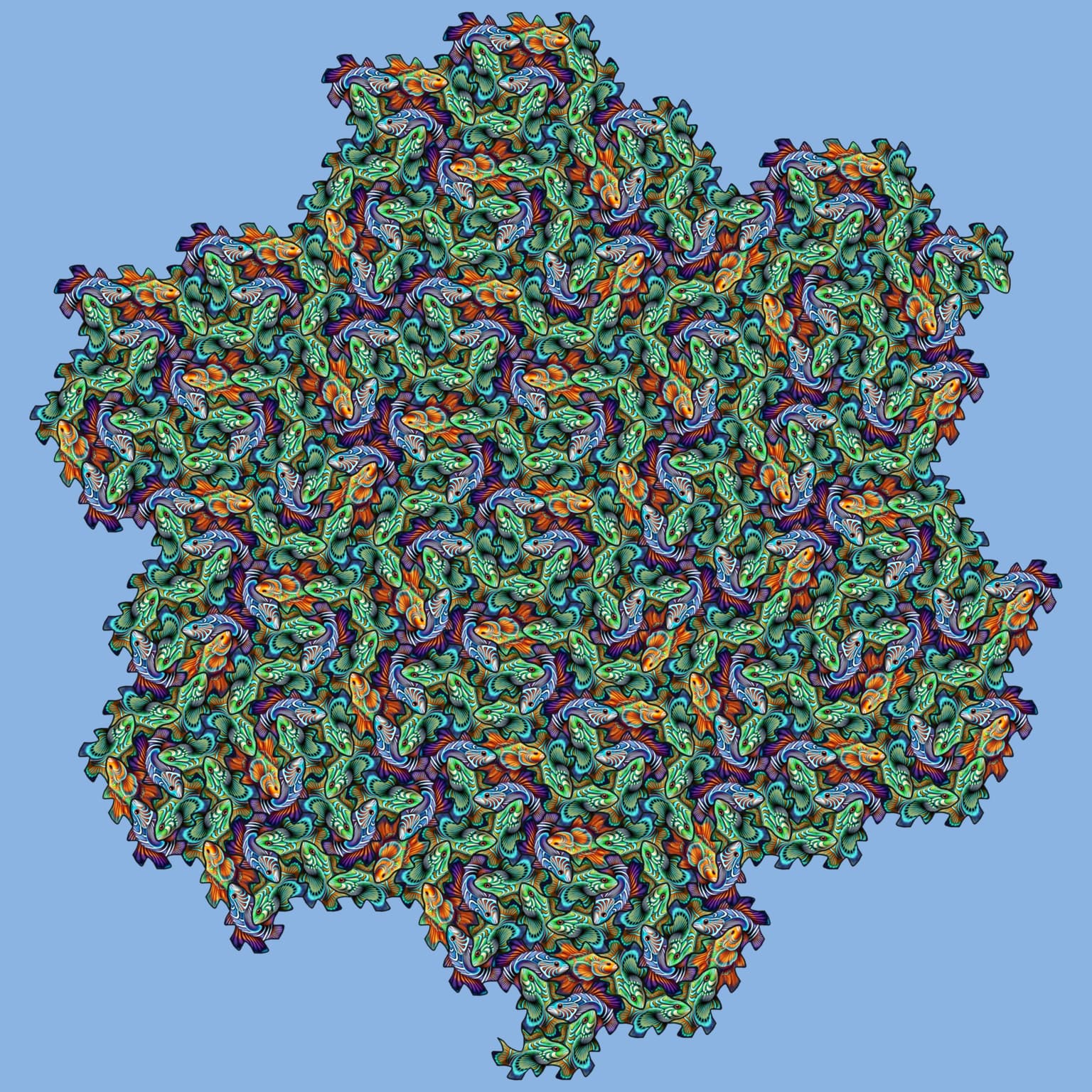
Gosper Mandarin Fish
60.0 x 60.0 x 1.0 cm
Gallery-bond
2025
The underlying structure of this tessellation is the well-known Gosper space-filling curve. The recently discovered Escheresque deformation scheme of the tiles [1] makes it easy to follow this curve, and any other such curve in a hexagonal grid. Three prototiles filled with fish are used: one for going straight (orange), one for turning 60 degrees left or right (greenish), and one for turning 120 degrees left or right (bluish). Microsoft CoPilot was asked to create Mandarin fish, but a significant amount of image processing was still required to make the fish fit in the outlines of the prototiles.
[1] T. Veugen. “Tessellations from Space-Filling Curves.” Bridges Conference Proceedings, Eindhoven, The Netherlands, July 14-18, 2025.
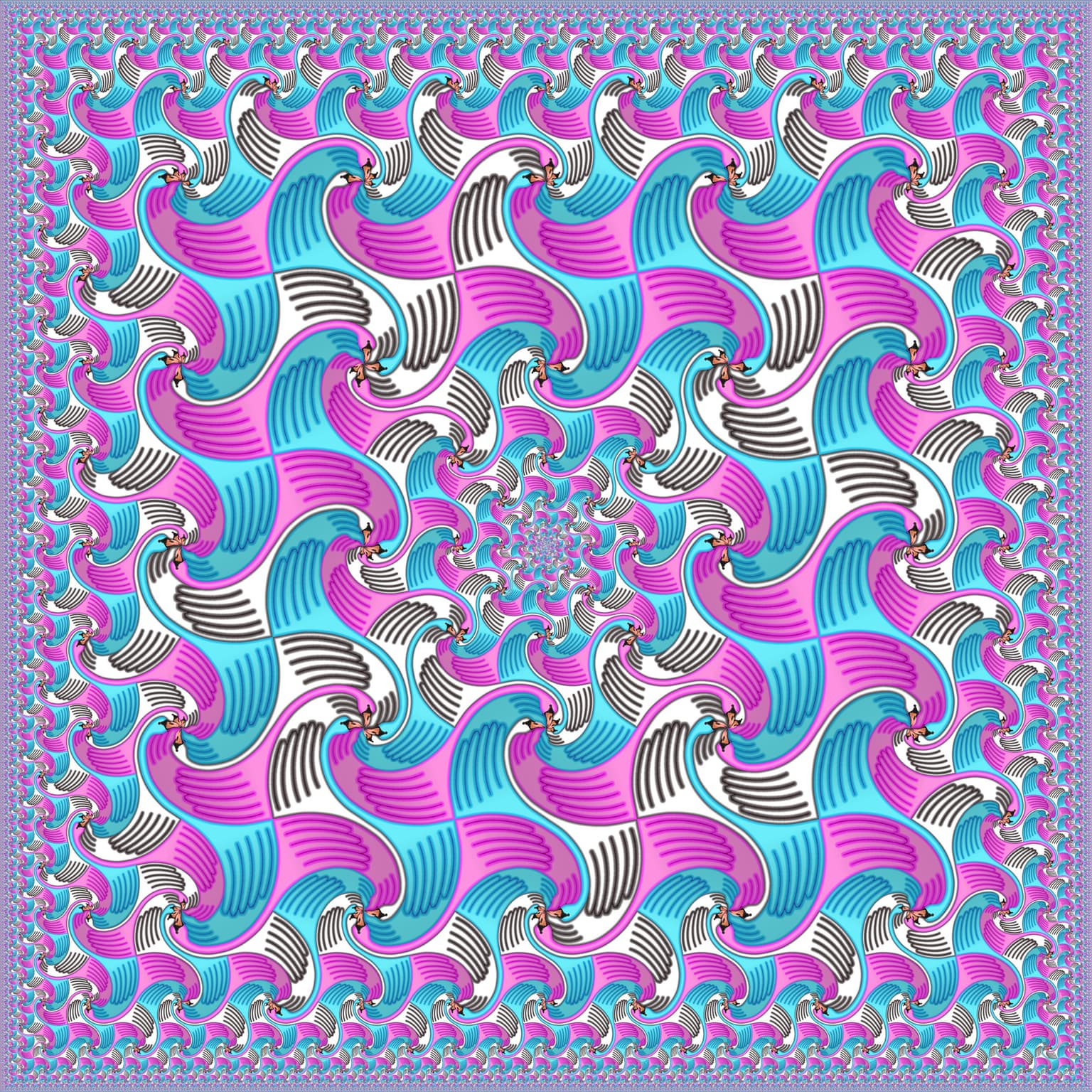
Swans Square Fractal
50.0 x 50.0 x 1.0 cm
Gallery-bond
2023
The inspiration for this image comes from Escher's famous Square Limit, where part of the fish tiles are mirrored. In our image, the triangles of the tessellation are deformed into swans, which are only rotated and/or scaled, but not mirrored. Another major difference with Escher's artwork is the fractal structure to the center.
Escher investigated fractal behavior from a single central point, as shown in [1, p. 91]. His lecture illustration for showing fractal geometry [1, p. 252] actually contains exactly the same scheme of decreasing triangles as the scheme around the center in our figure!
[1] D. Schattschneider. Visions of Symmetry - Notebooks, Periodic Drawings, and Related Work of M. C. Escher. W. H. Freeman and Company, 1990